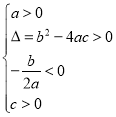题目内容
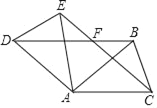
【题目】如图1,在等边△ABC中,点P是边BC上一动点(点P不与点B重合),且BP<PC,点B关于直线AP的对称点为D,连接CD、BD.
(1)依题意补全图形;
(2)若∠BAP=α,则∠BCD=______(用含α的式子表示);
(3)过点D作DE⊥DC,交直线AP于点E,连接EB、EC,判断△ABE的面积与△CDE的面积之间的数量关系,并证明.

【答案】(1)答案见解析;(2)α;(3)S△DEC=2S△ABE,证明见解析.
【解析】
(1)由题意画出图形;
(2)由轴对称的性质可得AP垂直平分BD,可得AB=AD=AC,∠BAP=∠PAD=α,由等腰三角形的性质可求解;
(3)由“SAS”可证△BAE≌△DAE,可得S△BAE=S△DAE,由等腰三角形的性质和平行线的性质可得S△DEC=2S△ABE.
(1)如图1所示;
(2)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°.
∵点B关于直线AP的对称点为D,
∴AP垂直平分BD,
∴AB=AD,且AP⊥BD,
∴∠BAP=∠PAD=α,
∴∠DAC=60°﹣2α.
∵AD=AC,
∴∠ACD![]() 60°+α,
60°+α,
∴∠BCD=α.
故答案为:α;
(3)S△DEC=2S△ABE,
理由如下:
如图2,过点A作AH⊥CD,连接EH,
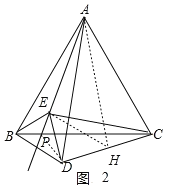
∵AC=AD,AH⊥CD,
∴DH=CH,
∴S△DEC=2S△DEH,
∵DE∥AH,
∴S△AED=S△DEH,
∵AB=AD,∠BAE=∠DAE,AE=AE,
∴△BAE≌△DAE(SAS),
∴S△BAE=S△DAE,
∴S△DEC=2S△ABE.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
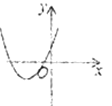
方程有两个不相等的负实根 |
|
|
____________ |
|
|
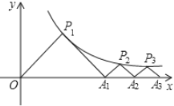
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.