题目内容
7.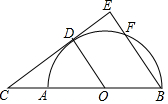 如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接OD.作BE⊥CD于点E,交半圆O于点F.已知CE=12,BE=9.
如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接OD.作BE⊥CD于点E,交半圆O于点F.已知CE=12,BE=9.(1)求证:△COD∽△CBE.
(2)求半圆O的半径r的长.
分析 (1)由切线的性质和垂直的定义得出∠E=90°=∠CDO,再由∠C=∠C,得出△COD∽△CBE.
(2)由勾股定理求出BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=15,由相似三角形的性质得出比例式,即可得出答案.
解答 (1)证明:∵CD切半圆O于点D,
∴CD⊥OD,
∴∠CDO=90°,
∵BE⊥CD,
∴∠E=90°=∠CDO,
又∵∠C=∠C,
∴△COD∽△CBE.
(2)解:在Rt△BEC中,CE=12,BE=9,
∴BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=15,
∵△COD∽△CBE.
∴$\frac{OD}{BE}=\frac{OC}{BC}$,即$\frac{r}{9}=\frac{15-r}{15}$,
解得:r=$\frac{45}{8}$.
点评 本题考查了切线的性质、相似三角形的判定及其性质、勾股定理;熟练掌握相似三角形的判定与性质是解决问题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
18.根据PM2.5空气质量标准:24小时PM2.5均值在0∽35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表,这组PM2.5数据的中位数是( )
| 天数 | 3 | 1 | 1 | 1 | 1 |
| PM2.5 | 18 | 20 | 21 | 29 | 30 |
| A. | 21微克/立方米 | B. | 20微克/立方米 | C. | 19微克/立方米 | D. | 18微克/立方米 |
15.下列计算正确的是( )
| A. | 2a+b=2ab | B. | (-a)2=a2 | C. | a6÷a2=a3 | D. | a3•a2=a6 |
12. 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )
 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
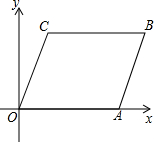 如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是(7,4).
如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是(7,4). 如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°.
如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°.