题目内容
18.计算:($\frac{1}{3}$)-2-2+(π-2014)0+sin60°+|$\sqrt{3}-2$|分析 本题涉及负整数指数幂、零指数幂、特殊角的三角函数值、绝对值四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:($\frac{1}{3}$)-2-2+(π-2014)0+sin60°+|$\sqrt{3}-2$|
=9-2+1+$\frac{\sqrt{3}}{2}$+2-$\sqrt{3}$
=10-$\frac{\sqrt{3}}{2}$.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、绝对值等考点的运算.

练习册系列答案
相关题目
9.函数y=kx与y=-$\frac{k}{x}$在同一坐标系内的大致图象是( )
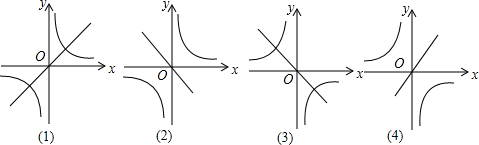

| A. | (1)和(2) | B. | (1)和(3) | C. | (2)和(3) | D. | (2)和(4) |
6.能用平方差公式进行计算的是( )
| A. | (2a-b)(-b+2a) | B. | (a-2b)(2a+b) | C. | (-2a-b)(2a+b) | D. | (-2a-b)(-2a+b) |
7.下列说法正确的是( )
| A. | 三角形的中线就是过顶点平分对边的直线 | |
| B. | 三角形的三条角平分线的交点有可能在三角形外部 | |
| C. | 三角形的三条高线的交点必在三角形内部 | |
| D. | 以上说法都错 |
8.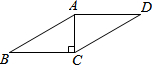 如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
 如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )| A. | $8+4\sqrt{3}$ | B. | $4+2\sqrt{3}$ | C. | 8 | D. | 4 |