题目内容
17.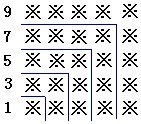 探索规律:观察下面由※组成的图案和算式,解答问题:
探索规律:观察下面由※组成的图案和算式,解答问题:1+3=4=22
1+3+5=9=32
1+3+5+7=19=42
1+3+5+7+9=25=52
(1)请猜想1+3+5+7+9+…+19=100;
(2)1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=(n+2)2;
(3)请用上述规律计算:51+53+55+…+2011+2013.
分析 (1)根据已知得出连续奇数的和等于数字个数的平方;
(2)根据已知得出连续奇数的和等于数字个数的平方,得出答案即可;
(3)利用以上已知条件得出51+53+55+…+2011+2013=(1+3+5+…+2007+2013)-(1+3+5+…+49),求出即可.
解答 解:(1)由已知得出:
1+3=4=22
1+3+5=9=32
1+3+5+7=19=42
1+3+5+7+9=25=52
依此类推:第n个所代表的算式为:1+3+5+…+(2n-1)=n2;
(1)当2n-1=19,即n=10时,1+3+5+…+19=102.
(2)($\frac{2n+3+1}{2}$)2=(n+2)2;
(3)51+53+55+…+2011+2013
03+105+107+…+2007+2009,
=(1+3+5+…+2011+2013)-(1+3+5+…+49)
=($\frac{2013+1}{2}$)2-($\frac{49+1}{2}$)2=10052-512
=10072-252
=1003104.
故答案为:100,(n+2)2.
点评 此题主要考查了数字变化规律,培养学生通过特例分析从而归纳总结出一般结论的能力.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目的难点.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
7.如果a、b互为相反数,x、y互为倒数,则|a+b-xy|等于( )
| A. | 0 | B. | 2 | C. | 1 | D. | -1 |
5. 我们用如图的方法来修理一条摇晃的凳子是根据( )
我们用如图的方法来修理一条摇晃的凳子是根据( )
 我们用如图的方法来修理一条摇晃的凳子是根据( )
我们用如图的方法来修理一条摇晃的凳子是根据( )| A. | 两点之间线段最短 | B. | 矩形的对称性 | ||
| C. | 矩形的四个角都是直角 | D. | 三角形具有稳定性 |
12.在-$\sqrt{4}$,3.14,π,$\sqrt{10}$,1.$\stackrel{•}{5}$$\stackrel{•}{5}$,$\frac{2}{7}$中无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 |
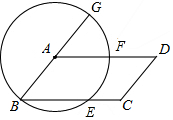 如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断$\widehat{EF}$和$\widehat{FG}$是否相等,并说明理由.
如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断$\widehat{EF}$和$\widehat{FG}$是否相等,并说明理由.