题目内容
11.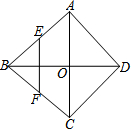 如图,菱形ABCD的对角线AC、BD相交于O点,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC、BD相交于O点,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )| A. | 5 | B. | $4\sqrt{6}$ | C. | $4\sqrt{7}$ | D. | 20 |
分析 由菱形的性质得出AB=BC=CD=AD,AC⊥BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD=2,证出EF是△ABC的中位线,由三角形中位线定理得出AC=2EF=2$\sqrt{3}$,得出OA=$\sqrt{3}$,由勾股定理求出AB,即可求出菱形的周长.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD=2,
∴∠AOB=90°,
∵E、F分别是AB、BC边上的中点,
∴EF是△ABC的中位线,
∴AC=2EF=2$\sqrt{3}$,
∴OA=$\sqrt{3}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{7}$,
∴菱形ABCD的周长=4AB=4$\sqrt{7}$;
故选C.
点评 本题考查了菱形的性质、三角形中位线定理、勾股定理;熟练掌握菱形的性质,由三角形中位线定理得出AC,由勾股定理求出AB是解决问题的关键.

练习册系列答案
相关题目
19.在平面直角坐标系中,函数y=x2-2x的图象为C1,C1关于原点对称的图象为C2,则直线y=a(a为常数)与C1、C2的交点共有( )
| A. | 2个 | B. | 1个或2个或3个 | ||
| C. | 2个或3个或4个 | D. | 1个或2个或3个或4个 |
6.不等式组$\left\{\begin{array}{l}\frac{1}{2}x-1<\frac{x}{3}\;,\;\;\\ 2x-4<3x+3.\end{array}\right.$的解集为( )
| A. | -7<x<6 | B. | -7<x<1 | C. | x<1 | D. | x<6 |
3.已知三角形的两边长为5,9,则第三边的长度可能是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20. 如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )
如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )
 如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )
如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
1.多项式1+2xy-3xy2的次数及最高次项的系数分别是( )
| A. | 5,-3 | B. | 2,-3 | C. | 2,3 | D. | 3,-3 |
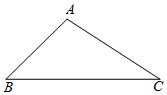 如图,在△ABC中,∠B=45°,∠C=30°,AB=4$\sqrt{2}$,求AC和BC的长.
如图,在△ABC中,∠B=45°,∠C=30°,AB=4$\sqrt{2}$,求AC和BC的长.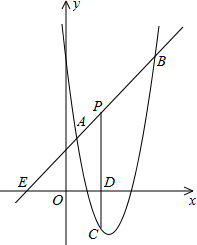 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.