题目内容
8.下列计算中结果正确的题号是①:①$\sqrt{18}-\sqrt{32}=-\sqrt{2}$;②${({-3})^{-2}}=-\frac{1}{9}$;③$\sqrt{{{({-2})}^2}}=-2$;④2cos30°+|1-tan60°|=1.
分析 ①先化简二次根式,然后再合并即可;②依据负整数指数幂的性质计算即可;③利用二次根式的性质化简即可;④将特殊角的三角函数值代入计算即可.
解答 解:$\sqrt{18}$-$\sqrt{32}$=3$\sqrt{2}$-4$\sqrt{2}$=-$\sqrt{2}$,故①正确;
(-3)-2=$\frac{1}{9}$,故②错误;
$\sqrt{(-2)^{2}}$=|-2|=2,故③错误;
2cos30°+|1-tan60°|=2×$\frac{\sqrt{3}}{2}$+|1-$\sqrt{3}$|=$\sqrt{3}$+$\sqrt{3}$-1=2$\sqrt{3}$-1,故④错误.
故答案为:①.
点评 本题主要考查的是实数的运算,熟练掌握实数的运算法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )
如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )
 如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )
如图,一次函数y=kx+b图象经过(1,0),(0,2),则不等式kx+b>0的解为( )| A. | x>1 | B. | x<1 | C. | x>2 | D. | x<2 |
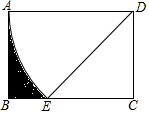 如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=2,以D为圆心,AD为半径画弧交线段BC于E,则阴影部分的面积为$\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π.
如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=2,以D为圆心,AD为半径画弧交线段BC于E,则阴影部分的面积为$\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π.