题目内容
13.当a>0且x>0时,因为${(\sqrt{x}-\frac{{\sqrt{a}}}{{\sqrt{x}}})^2}≥0$,所以$x-2\sqrt{a}+\frac{a}{x}≥0$,从而$x+\frac{a}{x}≥2\sqrt{a}$(当$x=\sqrt{a}$时取等号).记函数$y=x+\frac{a}{x}(a>0,x>0)$,由上述结论可知:当$x=\sqrt{a}$时,该函数有最小值为$2\sqrt{a}$.
(1)已知函数y1=x(x>0)与函数${y_2}=\frac{8}{x}(x>0)$,则当x=2$\sqrt{2}$时,y1+y2取得最小值为4$\sqrt{2}$;
(2)已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共360元;二是燃油费,每千米为1.6元;三是折旧费,它与路程的平方成正比,比例系数为0.001.设该汽车一次运输的路程为x千米,求当x为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
分析 (1)根据题目提示的方法确定取得最值时x的值即可;
(2)根据运输成本的组成列式表示出汽车平均每千米的运输成本,然后根据知识迁移的方法解答即可.
解答 解:(1)由题意得:a=8,
∵当$x=\sqrt{a}$时,该函数有最小值为$2\sqrt{a}$,
∴当x=$\sqrt{a}$=$\sqrt{8}$=2$\sqrt{2}$时,y1+y2取得最小值为2$\sqrt{a}$=4$\sqrt{2}$;
(2)设该汽车平均每千米的运输成本为y元,
由题意,$y=\frac{{0.001{x^2}+1.6x+360}}{x}=0.001x+\frac{360}{x}+1.6$=$0.001(x+\frac{360000}{x})+1.6$.
当$x=\sqrt{360000}=600$千米时,该汽车平均每千米的运输成本y最低,
最低成本为$0.001×2\sqrt{360000}+1.6=2.8$元.
点评 本题考查了二次根式的应用及反比例函数的综合知识,读懂题目信息,理解知识迁移中的最小值的求法是解题的关键.

练习册系列答案
相关题目
2.已知不等式2x+a≥0的负整数解恰好是-3,-2,-1,那么a满足条件( )
| A. | a=6 | B. | a≥6 | C. | a≤6 | D. | 6≤a<8 |
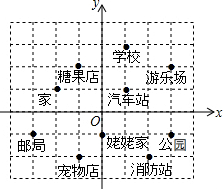 下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.
下图中标明了小红家附近的一些地方,建立平面直角坐标系如图. 如图,梯形OABC中,CB∥OA,O为坐标原点,B(2,4),C(0,4),tan∠BAO=2,动点Q 从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点Q作OP⊥x轴交折线C-B-A于点P,以PQ为一边向左作正方形PQRS,设运动时间为t (秒),正方形PQRS与梯形OABC重叠的面积为S(平方单位).
如图,梯形OABC中,CB∥OA,O为坐标原点,B(2,4),C(0,4),tan∠BAO=2,动点Q 从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点Q作OP⊥x轴交折线C-B-A于点P,以PQ为一边向左作正方形PQRS,设运动时间为t (秒),正方形PQRS与梯形OABC重叠的面积为S(平方单位).
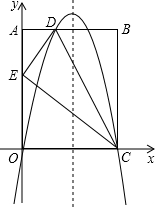 如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.