��Ŀ����
5����֪����ͼ��1������ƽ���ı���ABCD�У�AB=12��BC=6��AD��BD����DΪб����ƽ���ı���ABCD���ڲ���Rt��AED����EAD=30�㣬��AED=90�㣮��1�����AED���ܳ���
��2����Rt��AED��ÿ��2����λ���ȵ��ٶ�������DC�����ƶ�����Rt��AED���BDCû���ص�����ʱֹͣ�˶������˶���ʱ��Ϊt�룬Rt��AED���BDC�ص����ֵ����ΪS����ֱ��д��S��t�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3����ͼ��2�����ڣ�2���У���Rt��AEDֹͣ�ƶ������Ƶ�C˳ʱ����ת����0�㣼����180�㣩������ת�����У�B�Ķ�Ӧ��ΪB�䣬��E�Ķ�Ӧ��ΪE�䣬��ֱ��B��E����ֱ��BE���ڵ�P����ֱ��CB���ڵ�Q���Ƿ���������Ħ���ʹ��BPQΪ���������Σ������ڣ�������Ķ������������ڣ���˵�����ɣ�

���� ��1����Rt��ADE�У���ֱ�������μ��ɣ�
��2���ڡ�AED����ƽ�ƵĹ����У�
��I����0��t��1.5ʱ�����ͼ1��ʾ����ʱ�ص�����Ϊһ�������Σ�
��II����1.5��t��4.5ʱ�����ͼ2��ʾ����ʱ�ص�����Ϊһ���ı��Σ�
��III����4.5��t��6ʱ�����ͼ3��ʾ����ʱ�ص�����Ϊһ������Σ�
��3��������ת�͵��������ε����ʽ���̽���������ǣ����ڦ���30���75�㣩��ʹ��BPQΪ���������Σ����ͼ4����ͼ5��ʾ��
��� �⣺��1�����ı���ABCD��ƽ���ı��Σ�
��AD=BC=6��
��Rt��ADE�У�AD=6����EAD=30�㣬
��AE=AD•cos30��=3$\sqrt{3}$DE=AD•sin30��=3$\sqrt{3}$��
���AED���ܳ�Ϊ��6+3+3=9+3$\sqrt{3}$��
��2���ڡ�AED����ƽ�ƵĹ����У�
��I����0��t��1.5ʱ�����ͼ1��ʾ����ʱ�ص�����Ϊ��D0NK��
��DD0=2t����ND0=DD0•sin30��=t��NK=ND0��tan30��=$\sqrt{3}$t��
��S=S��D0NK=$\frac{1}{2}$ND0•NK=t•$\sqrt{3}$t=$\frac{\sqrt{3}}{2}$t2��
��II����1.5��t��4.5ʱ�����ͼ2��ʾ����ʱ�ص�����Ϊ�ı���D0E0KN��
��AA0=2t����A0B=AB-AA0=12-2t��
��A0N=$\frac{1}{2}$A0B=6-t��NK=A0N•tan30��=$\frac{\sqrt{3}}{3}$��6-t����
��S=S�ı���D0E0KN=S��A0D0E0-S��A0NK=$\frac{1}{2}$��3��3$\sqrt{3}$-$\frac{1}{2}$����6-t����$\frac{\sqrt{3}}{3}$��6-t��=-$\frac{\sqrt{3}}{6}$t2+2$\sqrt{3}$t-$\frac{3\sqrt{3}}{2}$��
��III����4.5��t��6ʱ�����ͼ3��ʾ����ʱ�ص�����Ϊ�����D0IJKN��
��AA0=2t����A0B=AB-AA0=12-2t=D0C��
��A0N=$\frac{1}{2}$A0B=6-t��D0N=6-��6-t��=t��BN=A0B•cos30��=$\sqrt{3}$��6-t����
��֪CI=BJ=A0B=D0C=12-2t��
��BI=BC-CI=2t-6��
S=S����BND0I-S��BKJ=$\frac{1}{2}$[t+��2t-6��]•$\sqrt{3}$��6-t��-$\frac{1}{2}$•��12-2t��•$\frac{\sqrt{3}}{3}$��12-2t��=-$\frac{13\sqrt{3}}{6}$t2+20$\sqrt{3}$t-42$\sqrt{3}$��
����������S��t֮��ĺ�����ϵʽΪ��
S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{t}^{2}��0��t��1.5��}\\{-\frac{\sqrt{3}}{6}{t}^{2}+2\sqrt{3}t-\frac{3\sqrt{3}}{2}��1.5��t��4.5��}\\{-\frac{13\sqrt{3}}{6}{t}^{2}+20\sqrt{3}t-42\sqrt{3}��4.5��t��6��}\end{array}\right.$��
��3�����ڦ���ʹ��BPQΪ���������Σ�
�������£���̽�����á�BPQ�ס�B1QC��
�ʵ���BPQΪ����������ʱ����B1QCҲΪ���������Σ�
��I����QB=QPʱ�����ͼ4����
��QB1=QC�����B1CQ=��B1=30�㣬
����BCB1=30�㣬
���=30�㣻
��II����BQ=BPʱ����B1Q=B1C��
����Q���߶�B1E1���ӳ�����ʱ�����ͼ5����
�ߡ�B1=30�㣬���B1CQ=��B1QC=75�㣬
����BCB1=75�㣬
���=75�㣻
����Q���߶�E1B1���ӳ�����ʱ�����ͼ6����
�ߡ�B1=30�㣬���B1CQ=��B1QC=15�㣬
����BCB1=180��-��B1CQ=180��-15��=165�㣬
���=165�㣮
�������������ڦ�=30�㣬75���165�㣬ʹ��BPQΪ���������Σ�
���� ���⿼�����˶����뼸�α任�ۺ��⣬�ѶȽϴ��ѵ����ڣ���һ���ڣ�2���ʵ��˶��������У����������ε��˶����̣���ȷ��ͬʱ�ε��ص�ͼ����״���ǽ����ѵ㣻������ڣ�3���ʵĴ����������У�̽���������������ת�ǣ������������ز�©���ǽ����ѵ㣻����������ڣ�2�����У��������ܴ�����ʧ�֣�

 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�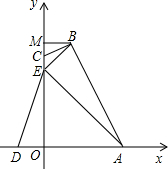 ��ͼ���ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�����B��BM��y�ڵ�M��OE=OA=3��OD=1������AE��BE��DE����֪tan��CBE=$\frac{1}{3}$��B��1��4����
��ͼ���ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�����B��BM��y�ڵ�M��OE=OA=3��OD=1������AE��BE��DE����֪tan��CBE=$\frac{1}{3}$��B��1��4����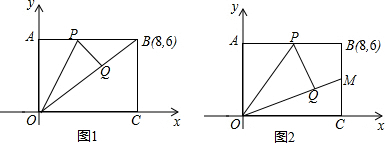
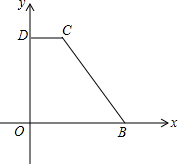 ��ͼ����ƽ��ֱ������ϵ�У���BΪx����������һ�㣬��DΪy����������һ�㣬CD��OB��OB=14��CD=2��BC=13����������E��Fͬʱ��O����������е�E��ÿ��1����λ���ٶ�������O��D��C�ƶ�����F��ÿ��2����λ���ٶȴӵ�O���B�ƶ���
��ͼ����ƽ��ֱ������ϵ�У���BΪx����������һ�㣬��DΪy����������һ�㣬CD��OB��OB=14��CD=2��BC=13����������E��Fͬʱ��O����������е�E��ÿ��1����λ���ٶ�������O��D��C�ƶ�����F��ÿ��2����λ���ٶȴӵ�O���B�ƶ��� ��ͼ���������������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ����Ϊ��㣮�����ڸ�����5��5�������������У��Ը��Ϊ���㣬�����ĸ�ֱ�������Σ����ĸ�ֱ�������ε�б�߳��ֱ�Ϊ$\sqrt{5}$��$2\sqrt{2}$��$\sqrt{10}$��$\sqrt{13}$�������������ĸ�ֱ�������γ�����ͱ߿����غ��⣬���ಿ�ֲ����غϣ���
��ͼ���������������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ����Ϊ��㣮�����ڸ�����5��5�������������У��Ը��Ϊ���㣬�����ĸ�ֱ�������Σ����ĸ�ֱ�������ε�б�߳��ֱ�Ϊ$\sqrt{5}$��$2\sqrt{2}$��$\sqrt{10}$��$\sqrt{13}$�������������ĸ�ֱ�������γ�����ͱ߿����غ��⣬���ಿ�ֲ����غϣ���