题目内容
已知等腰Rt△ABC的直角边长为
,将等腰三角形绕斜边旋转一周,求所得的几何体的全面积.
| 2 |
考点:圆锥的计算,等腰直角三角形
专题:
分析:易得此几何体为圆锥,那么表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
解答: 解:作BF⊥AC,
解:作BF⊥AC,
由题意知,∵在Rt△ABC中,∠ACB=90°,AB=BC=
cm,
∴AC2=AB2+BC2=4,
∴AC=2,
以BF为半径的圆的周长=2π×
=2
π,
得到的几何体表面积为
×2
π(AB+BC)=
×2
π×2
=4π.
 解:作BF⊥AC,
解:作BF⊥AC,由题意知,∵在Rt△ABC中,∠ACB=90°,AB=BC=
| 2 |
∴AC2=AB2+BC2=4,
∴AC=2,
以BF为半径的圆的周长=2π×
| 2 |
| 2 |
得到的几何体表面积为
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:此题主要考查了圆锥侧面积的计算,关键是利用圆锥的侧面积=底面周长×母线长÷2得出.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
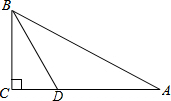 在Rt△ABC中,∠A=30°,∠C=90°,∠BDC=60°,BC=6cm,求AD的长.
在Rt△ABC中,∠A=30°,∠C=90°,∠BDC=60°,BC=6cm,求AD的长. 如图为某工厂生产的零件的示意图,请根据图中提供的信息,计算这个零件的体积.
如图为某工厂生产的零件的示意图,请根据图中提供的信息,计算这个零件的体积.