题目内容
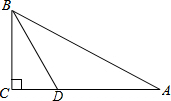在Rt△ABC中，∠A=30°，∠C=90°，∠BDC=60°，BC=6cm，求AD的长．考点：含30度角的直角三角形,勾股定理
专题：
分析：根据30°角所对直角边为斜边的一半可得BD=2CD，AB=2BC，即可解题．
解答：解：∵∠CBD=30°，∠A=30°，
∴AB=2BC，BD=2CD，
∵BC2+CD2=BD2，BC2+AC2=AB2，
∴CD=2
，BD=4
，AB=2BC=12，AC=6
，
∴AD=AC-CD=4
．
∴AB=2BC，BD=2CD，
∵BC2+CD2=BD2，BC2+AC2=AB2，
∴CD=2
| 3 |
| 3 |
| 3 |
∴AD=AC-CD=4
| 3 |
点评：本题考查了30°角所对直角边为斜边的一半的性质，考查了勾股定理的运用，本题中求AC的长是解题的关键．
练习册系列答案
相关题目
下列各式中，可以作为因式分解最后结果的是（ ）
| A、a（2a-4b）（2a+4b） |
| B、[a+2（a+b）][a-2（a+b）] |
| C、-（x2+1）（x-1） |
| D、（a-b）（a+b）（a-b） |