题目内容
在△ABC中，三边分别为AB=3，BC=4，AC=6，则△ABC三边依次对应高的比为 ．
考点：三角形的面积
专题：
分析：设边AB、BC、AC上对应高分别为h1，h2，h3，则由三角形的面积公式来求它们的比值．
解答：
解：设边AB、BC、AC上对应高分别为h1，h2，h3，则
AB•h1=
BC•h2=
AC•h3，即AB•h1=BC•h2=AC•h3，
∵AB=3，BC=4，AC=6，
∴3h1=4h2=6h3，
∴h1：h2：h3=4：3：2．
故答案是：4：3：2．
解：设边AB、BC、AC上对应高分别为h1，h2，h3，则| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=3，BC=4，AC=6，
∴3h1=4h2=6h3，
∴h1：h2：h3=4：3：2．
故答案是：4：3：2．
点评：本题考查了三角形的面积．此题利用三角形的面积是定值列出的等式AB•h1=BC•h2=AC•h3．
练习册系列答案
阅读快车系列答案
相关题目
如图，画出△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1．
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，则∠A的余角是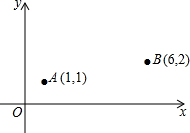
已知A（1，1），B（6，2），C、D分别为x轴、y轴上的动点，在运动的过程中，如果C、D满足|AC-BC|最大，而使|AD+BD|最小，则CD的长为
在某公益活动中，小明对本班同学的捐款情况进行了统计，绘制成如图所示的不完整的统计图，其中捐100元的人数占全班总人数的25%，则全班本次参与捐款的共有
如图，∠ACD=∠BCD，DE∥BC交AC于E．若∠ACB=60°，∠B=74°，则∠EDC=若直线y=3x-1与y=x-t的交点在第四象限，则常数t的取值范围是（ ）
A、t＜
| ||
B、
| ||
| C、t＞1 | ||
D、t＞1或t＜
|