Question

（1）解方程组

y=x+1 x2+y2=1

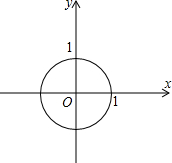
（2）已知：如图所示，圆O的圆心为原点，半径为1，请在图中画出一次函数
y=x+1的图象，并写出它与圆O的交点坐标（无需过程）；
（3）你能发现（1）中方程组的解与（2）中交点坐标之间的关系吗？请写出你的发现，不用说明理由．

Answer 1

考点：圆的综合题

专题：

分析：（1）利用用代入消元法解出二元一次方程组即可；
（2）利用一次函数图象画法得出函数图象，进而得出它与圆O的交点坐标；
（3）利用（1）中所求1，结合（2）的交点，进而得出发现．

解答：解：（1）

y=x+1① x2+y2=1②

把①代入②，整理，
得x²+x=0，
解得：x₁=-1，x₂=0，
把x₁=-1代入（1），得y₁=0，
把x₂=0代入①，得y₂=1，
所以原方程组的解是：

x1=-1 y1=0

，

x2=0 y2=1

；

（2）如图所示：
当y=0，x=-1，x=0时，y=1，

交点坐标为（-1，0）、（0，1）；

（3）（1）中方程组的解就是（2）中交点的坐标．
①设点P（x，y），则OP=

x2+y2

，所以x²+y²=1表示的图形是以圆心为原点，半径为1的圆；
②类比“两条直线的交点坐标就是它们的解析式组成方程组的解”，
发现：“直线与圆的交点坐标就是它们的解析式组成方程组的解”．

点评：此题主要考查了二元一次方程组的解法以及一次函数图象画法等知识，利用数形结合得出是解题关键．