题目内容
14.解方程:(1)$\frac{x}{x-3}$=$\frac{x-1}{x+1}$;
(2)$\frac{2-x}{x-3}$+3=$\frac{2}{3-x}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x2+x=x2-4x+3,
解得:x=$\frac{3}{5}$,
经检验x=$\frac{3}{5}$是分式方程的解;
(2)去分母得:2-x+3x-9=-2,
解得:x=$\frac{5}{2}$,
经检验x=$\frac{5}{2}$是分式方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
2.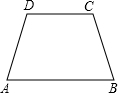 如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )
如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )
 如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )
如图,等腰梯形ABCD中,AB∥DC,AD=BC=4,AB=7,CD=5,则梯形ABCD的面积是( )| A. | 6$\sqrt{15}$ | B. | 12$\sqrt{15}$ | C. | 6$\sqrt{17}$ | D. | 6$\sqrt{5}$ |
6.已知a+$\frac{1}{a}$=$\sqrt{10}$,则a-$\frac{1}{a}$的值为( )
| A. | 2 | B. | 6 | C. | ±$\sqrt{6}$ | D. | ±2$\sqrt{2}$ |

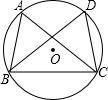 如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB.
如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB.
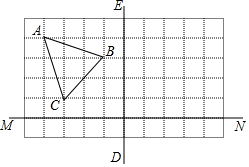 如图,在所给正方形网格图中完成下列各题:
如图,在所给正方形网格图中完成下列各题: