题目内容
12. 如图,在△ABC中,点D、E在BC上,AB=BE,AC=CD,已知∠BAC=100°,求∠DAE的大小.
如图,在△ABC中,点D、E在BC上,AB=BE,AC=CD,已知∠BAC=100°,求∠DAE的大小.
分析 根据等腰三角形性质得出∠BAE=∠BEA,∠CAD=∠CDA,根据三角形内角和定理得出∠B=180°-2∠BAE①,∠C=180°-2∠CAD②,①+②得出∠B+∠C=360°-2(∠BAE+∠CAD),求出2∠DAE=180°-∠BAC,代入求出即可.
解答 解:∵BE=BA,
∴∠BAE=∠BEA,
∴∠B=180°-2∠BAE,①
∵CD=CA,
∴∠CAD=∠CDA,
∴∠C=180°-2∠CAD,②
①+②得:∠B+∠C=360°-2(∠BAE+∠CAD)
∴180°-∠BAC=360°-2[(∠BAD+∠DAE)+(∠DAE+∠CAE)],
∴-∠BAC=180°-2[(∠BAD+∠DAE+∠CAD)+∠DAE],
∴-∠BAC=180°-2(∠BAC+∠DAE),
∴2∠DAE=180°-∠BAC.
∵∠BAC=100°,
∴2∠DAE=180°-100°=80°,
∴∠DAE=40°.
点评 本题考查了三角形内角和定理,等腰三角形的性质的应用,关键是推出2∠DAE=180°-∠BAC.

练习册系列答案
相关题目
20.点P在第四象限,点P到x轴的距离是4,到y轴的距离是2,则点P的坐标是( )
| A. | (4,2) | B. | (4,-2) | C. | (-2,4) | D. | (2,-4) |
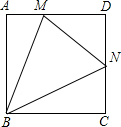 如图,在正方形ABCD中,N是DC的中点,M是AD上异于点D的点,且∠NMB=∠MBC,求$\frac{AM}{AB}$的值.
如图,在正方形ABCD中,N是DC的中点,M是AD上异于点D的点,且∠NMB=∠MBC,求$\frac{AM}{AB}$的值.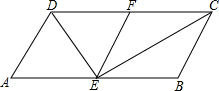 在四边形ABCD中,AD=BC,DE平分∠ADF,CE平分∠BCF,∠CDE+∠DCE=90°,E,F分别是AB,CD的中点.
在四边形ABCD中,AD=BC,DE平分∠ADF,CE平分∠BCF,∠CDE+∠DCE=90°,E,F分别是AB,CD的中点. 如图,△ABC三条角平分线AD、BE,CF交于点G,GH⊥BC于H,求证:∠BGD=∠CGH.
如图,△ABC三条角平分线AD、BE,CF交于点G,GH⊥BC于H,求证:∠BGD=∠CGH. 在同一平面直角坐标系中,画出函数y=-5x+1与y=0.5x-10的图象.
在同一平面直角坐标系中,画出函数y=-5x+1与y=0.5x-10的图象.