题目内容
13. 如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )
如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )| A. | $\sqrt{13}$ | B. | 6 | C. | 2$\sqrt{13}$ | D. | 10 |
分析 根据菱形的性质得AC⊥BD,OA=OC=$\frac{1}{2}$AC=6,OB=OD,则可根据勾股定理计算出OB=$\sqrt{13}$,然后利用BD=2OB求解.
解答 解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=6,OB=OD,
∴∠AOB=90°,
在Rt△AOB中,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{{7}^{2}-{6}^{2}}$=$\sqrt{13}$,
∴BD=2OB=2$\sqrt{13}$.
故选C.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.有3张背面相同的卡片,正面分别印有下列几种几何图形.现将这3张卡片正面朝下摆放,从中任意抽取一张后放回,再从中任意抽取一张,则两次抽到的卡片的正面图形都是中心对称图形的概率是( )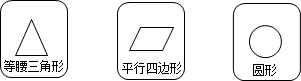

| A. | $\frac{2}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
2.圆锥的母线为6cm,底面半径为2cm,则圆锥的高为( )
| A. | $\sqrt{2}$cm | B. | 3$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4cm |
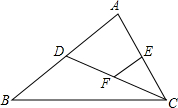 如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.
如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.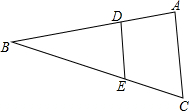 如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6.
如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6.