题目内容
9.(1)计算:-24-$\sqrt{12}$+|1-4sin60°|+(π-1)0;(2)先化简,再求值:(1-$\frac{3}{x+2}$)÷$\frac{x-1}{{x}^{2}+2x}$-$\frac{x}{x+1}$,其中x满足x2-x-1=0.
分析 (1)原式第一项利用乘方的意义化简,第二项化为最简二次根式,第三项利用特殊角的三角函数值及绝对值的代数意义化简,最后一项利用零指数幂法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,两项通分并利用同分母分式的减法法则计算得到最简结果,把已知等式变形后代入计算即可求出值.
解答 解:(1)原式=-16-2$\sqrt{3}$+2$\sqrt{3}$-1+1=-16;
(2)原式=$\frac{x+2-3}{x+2}$•$\frac{x(x+2)}{x-1}$-$\frac{x}{x+1}$=x-$\frac{x}{x+1}$=$\frac{{x}^{2}}{x+1}$,
由x2-x-1=0,得到x2-x=1,
则原式=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.有3张背面相同的卡片,正面分别印有下列几种几何图形.现将这3张卡片正面朝下摆放,从中任意抽取一张后放回,再从中任意抽取一张,则两次抽到的卡片的正面图形都是中心对称图形的概率是( )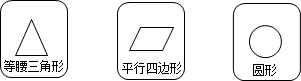

| A. | $\frac{2}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
19.一元一次方程组$\left\{\begin{array}{l}{x+3y=2}\\{x-2y=7}\end{array}\right.$的解的情况是( )
| A. | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=8}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=9}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$ |
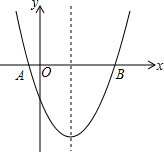 如图,已知抛物线y=x2-3x-$\frac{7}{4}$与x轴交于A、B两点.
如图,已知抛物线y=x2-3x-$\frac{7}{4}$与x轴交于A、B两点.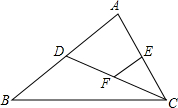 如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.
如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.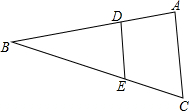 如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6.
如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6.