题目内容
4.先化简,再求值$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-{y}^{2}}$÷($\frac{1}{x}$-$\frac{1}{y}$),其中x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$.分析 根据分式的运算法则即可求出答案.
解答 解:原式=$\frac{(x-y)^{2}}{(x+y)(x-y)}$×$\frac{xy}{y-x}$
=-$\frac{x-y}{x+y}$×$\frac{xy}{x-y}$
=-$\frac{xy}{x+y}$
当x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$ xy=1,x+y=2$\sqrt{3}$
∴原式=-$\frac{\sqrt{3}}{6}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
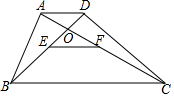 四边形ABCD中,AD∥BC,AC交BD于O,AD=5,BC=9,E,F分别是BD、AC的中点,下列结论正确的有①②④(填序号).
四边形ABCD中,AD∥BC,AC交BD于O,AD=5,BC=9,E,F分别是BD、AC的中点,下列结论正确的有①②④(填序号).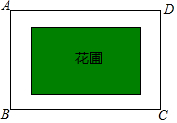 如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米. 如图是统计学生跳绳情况的频数分布直方图,如果跳 75次以上(含75次)为达标,则达标学生所占比例为90%.
如图是统计学生跳绳情况的频数分布直方图,如果跳 75次以上(含75次)为达标,则达标学生所占比例为90%.