题目内容
16. 如图所示,在矩形ABCD中,对角线AC、BD相交于点O,AE⊥BC于点E,BE:ED=1:3,AD=6cm,求AE的长.
如图所示,在矩形ABCD中,对角线AC、BD相交于点O,AE⊥BC于点E,BE:ED=1:3,AD=6cm,求AE的长.
分析 先由矩形的性质和已知条件得出BE=OE,△ABO是等边三角形,得出∠ABO=60°,再得出∠ADE=30°,根据含30°的直角三角形的性质即可求出AE.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,OB=OD=$\frac{1}{2}$BD=AO,
∵BE:ED=1:3,
∴BE=OE,
∵AE⊥BC,
∴AB=AO,∠AED=90°,
∴AB=OB=AO,
∴∠ABO=60°,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD=3cm.
点评 本题考查了矩形的性质、等边三角形的判定与性质以及含30°的直角三角形的性质;证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
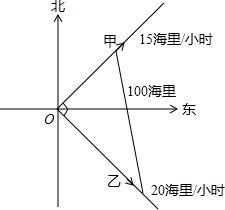 两条船同时从A港出发,一艘船的速度是15海里/时,航向是东北方向,另一艘船比它每小时快5海里,航向是东南方向,多少小时后两船相距100海里?
两条船同时从A港出发,一艘船的速度是15海里/时,航向是东北方向,另一艘船比它每小时快5海里,航向是东南方向,多少小时后两船相距100海里?