题目内容
19. 如图,四边形ABCD为菱形,对角线AB,CD相交于点O,∠CAD=30°,BD=6,求AB,AC的长.
如图,四边形ABCD为菱形,对角线AB,CD相交于点O,∠CAD=30°,BD=6,求AB,AC的长.
分析 利用已知条件易求AB的长,再由勾股定理可求出OA的长,进而可求对角线AC的长.
解答 解:∵四边形ABCD是菱形,且∠CAD=30°,
∴∠BAD=60°,AB=AD,
∴△ABD是正三角形,
∵BD=6,
∴AB=BD=6,
在Rt△AOB中,
∵OB=$\frac{1}{2}$AB,
∴OB=3,
∴AO2=AB2-OB2,
∴OA=3$\sqrt{3}$,
∴AC=2OA=6$\sqrt{3}$.
点评 本题主要考查的是菱形的性质:菱形的四条边都相等;对角线互相垂直平分;每条对角线平分一组对角.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
7.对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是( )
| A. | 通常不可互相转换 | |
| B. | 扇形统计图能清楚地表示出各部分在总体中所占的百分比 | |
| C. | 折线统计图能清楚地表示出每个项目的具体数目 | |
| D. | 条形统计图能清楚地反映事物的变化情况 |
14.平行四边形ABCD中,∠A:∠B:∠C:∠D可能是( )
| A. | 2:1:2:1 | B. | 1:2:2:1 | C. | 2:1:1:2 | D. | 1:2:3:4 |
4.对有理数x,y定义新运算:x?y=ax+by+1,其中a,b是常数.若2?(-1)=-3,3?3=4,则a,b的值分别为( )
| A. | a=1,b=2 | B. | a=-1,b=2 | C. | a=-1,b=-2 | D. | a=1,b=-2 |
11.一次函数y=kx+b的图象只经过第一、三象限,则( )
| A. | k>0 | B. | k<0 | C. | b>0 | D. | b<0 |
 如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为24,则BC的长为( )
如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为24,则BC的长为( )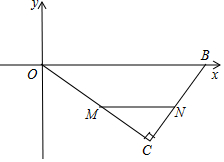 已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.
已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.