题目内容
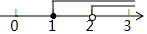
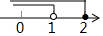
11．一次函数y=kx+b的图象只经过第一、三象限，则（ ）| A． | k＞0 | B． | k＜0 | C． | b＞0 | D． | b＜0 |
分析 根据一次函数y=kx+b的图象在坐标平面内的位置关系确定k，b的取值范围，从而求解．
解答 解：∵一次函数y=kx+b的图象经过第一、三象限，
∴k＞0，b=0，
综观各选项，可以选择A．
故选A．
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞0时，直线必经过一、三象限；k＜0时，直线必经过二、四象限．b＞0时，直线与y轴正半轴相交；b=0时，直线过原点；b＜0时，直线与y轴负半轴相交．
练习册系列答案
口算题天天练系列答案
相关题目
2．父子二人并排竖直站立于游泳池中时，爸爸露出水面的高度是他自身身高的$\frac{1}{3}$，儿子露出水面的高度是他自身身高的$\frac{1}{4}$，父子二人的身高之和为3.4米．若设爸爸的身高为x米，儿子的身高为y米，则可列方程组（ ）
| A． | $\left\{\begin{array}{l}{x+y=3.4}\\{\frac{1}{3}x=\frac{1}{4}y}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=3.4}\\{（1-\frac{1}{3}）x=\frac{1}{4}y}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=3.4}\\{\frac{1}{3}x=（1-\frac{1}{4}）y}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=3.4}\\{（1-\frac{1}{3}）x=（1-\frac{1}{4}）y}\end{array}\right.$ |
如图，四边形ABCD为菱形，对角线AB，CD相交于点O，∠CAD=30°，BD=6，求AB，AC的长．
16．
如图，在△ABC中，AB=3，BC=6，AC=4，点D，E分别是边AB，CB的中点，那么DE的长为（ ）
如图，在△ABC中，AB=3，BC=6，AC=4，点D，E分别是边AB，CB的中点，那么DE的长为（ ）| A． | 1.5 | B． | 2 | C． | 3 | D． | 4 |
3．每年四月北京很多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰．据测定，杨絮纤维的直径约为0.000 010 5米，将0.000 010 5用科学记数法可表示为（ ）
| A． | 1.05×105 | B． | 1.05×10-5 | C． | 0.105×10-4 | D． | 10.5×10-6 |
20．计算[（-a）2]3•（a3）2所得结果为（ ）
| A． | a10 | B． | -a10 | C． | a12 | D． | -a12 |
