题目内容
14.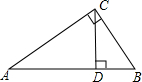 如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是( )
如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
分析 根据勾股定理,可得AB的长,根据三角形的面积公式,可得AD的长,根据勾股定理,可得BD的长,
解答 解:由勾股定理,得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
由三角形的面积,得
$\frac{1}{2}$AD•AB=$\frac{1}{2}$AC•BC,
解得AD=4.8,
cos∠BCD=$\frac{CD}{BC}$=$\frac{4.8}{6}$=$\frac{4}{5}$.
故选:D.
点评 本题考查了锐角三角函数的定义,利用了勾股定理,三角形的面积得出CD的长是解题关键.

练习册系列答案
相关题目
4.下列各组数中,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,1,2 | C. | 8,15,17 | D. | 5,12,23 |
9.下列说法正确的是( )
| A. | 延长射线OP | B. | 延长直线CD | C. | 延长线段CD | D. | 反向延长直线DC |
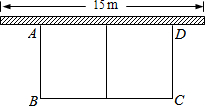 如图,某农场利用一面墙(墙长为15m)建养鸡场,用30m的围栏围成总面积为72m2的两个大小相同的矩形鸡圈,求养鸡场的两边AB,BC的长各为多少?
如图,某农场利用一面墙(墙长为15m)建养鸡场,用30m的围栏围成总面积为72m2的两个大小相同的矩形鸡圈,求养鸡场的两边AB,BC的长各为多少?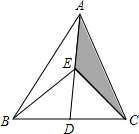 如图所示,在△ABC中,D、E分别为BC、AD的中点,且S△ABC=4,则S阴影=1.
如图所示,在△ABC中,D、E分别为BC、AD的中点,且S△ABC=4,则S阴影=1.



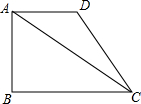 如图,四边形ABCD中,∠BAD=90°,∠ADC=135°,AB=8$\sqrt{3}$,BC=6$\sqrt{7}$,∠BAC=60°,求CD的长.
如图,四边形ABCD中,∠BAD=90°,∠ADC=135°,AB=8$\sqrt{3}$,BC=6$\sqrt{7}$,∠BAC=60°,求CD的长.