题目内容
19.下列各式:$\frac{2}{a}$,$\frac{4x}{π-3}$,$\frac{{x}^{2}-{y}^{2}}{2}$,$\frac{1}{x}+x$,$\frac{5{x}^{2}}{x+1}$,其中分式共有( )个.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据分式的定义对各式进行判断即可.
解答 解:下列各式:$\frac{2}{a}$,$\frac{4x}{π-3}$,$\frac{{x}^{2}-{y}^{2}}{2}$,$\frac{1}{x}+x$,$\frac{5{x}^{2}}{x+1}$,其中分式为下$\frac{2}{a}$,$\frac{1}{x}+x$,$\frac{5{x}^{2}}{x+1}$.
故选B.
点评 本题考查了分式的定义:一般地,如果A,B表示两个整式,并且B中含有字母,那么式子$\frac{A}{B}$叫做分式.

练习册系列答案
相关题目
14.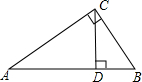 如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是( )
如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是( )
 如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是( )
如图,CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
4.近似数5.83×105是精确到( )
| A. | 百位 | B. | 千位 | C. | 百分位 | D. | 千分位 |
8.已知:|x|=3,|y|=2,且x>y,则x+y的值为( )
| A. | 5 | B. | 1 | C. | 5或1 | D. | -5或-1 |
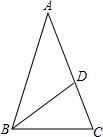 如图,在△ABC中,AB=AC,∠A=36°,点D在边AC上,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,点D在边AC上,BD平分∠ABC. 已知:如图,点A、B、C、D在同一条直线上,AE∥BF,AE=BF,AB=CD.求证:(1)CE=DF,
已知:如图,点A、B、C、D在同一条直线上,AE∥BF,AE=BF,AB=CD.求证:(1)CE=DF,