Question

11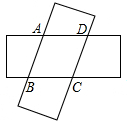．如图，用完全相同的两个矩形纸片交叉叠合得到四边形ABCD，则四边形ABCD的形状是菱形．

Answer 1

分析 先根据长方形的两组对边分别平行，得出AB∥CD，BC∥AD，证出四边形ABCD为平行四边形；再作?ABCD的两条高AE、AF，由两张长方形纸条的宽度相等，得出AE=AF，根据平行四边形的面积不变，证出?ABCD有一组邻边相等；从而根据定义得出四边形ABCD为菱形．

解答 解：∵两张纸条都是长方形，
∴AB∥CD，BC∥AD，
∴四边形ABCD为平行四边形．
过点A作AE⊥DC于E，AF⊥BC于F．
∵两张长方形纸条的宽度相等，
∴AE=AF．
又∵?ABCD的面积=DC•AE=BC•AF，
∴DC=BC，
∴?ABCD为菱形．
故答案是：菱形．

点评 本题主要考查学生对菱形判别方法的掌握；一个四边形为菱形的理论依据，常用三种方法：
①定义；②四边相等；③对角线互相垂直平分．