题目内容
17.在Rt△ABC中,∠C=Rt∠,根据下列条件求各个锐角(精确到1′).(1)AB=3,AC=1
(2)AC=5,BC=4.
分析 (1)利用∠A的余弦求出∠A的值,根据直角三角形两锐角互余求出∠B的值,即可解题;
(2)利用∠A的正切求出∠A的值,根据直角三角形两锐角互余求出∠B的值,即可解题.
解答 解:(1)∵在Rt△ABC中,∠C=Rt∠,AB=3,AC=1,
∴cos∠A=$\frac{AC}{AB}$=$\frac{1}{3}$,
∴∠A≈70°32′,
∴∠B=90°-∠A≈19°28′; (2)∵在Rt△ABC中,∠C=Rt∠,AC=5,BC=4,
(2)∵在Rt△ABC中,∠C=Rt∠,AC=5,BC=4,
∴tan∠A=$\frac{BC}{AC}$=$\frac{4}{5}$,
∴∠A≈38°40′,
∴∠B=90°-∠A≈52°20′.
点评 本题考查了解直角三角形,直角三角形两锐角互余的性质,掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,△ABC的顶点在网格纸的格点上,则cos∠A=$\frac{2\sqrt{5}}{5}$.
如图,△ABC的顶点在网格纸的格点上,则cos∠A=$\frac{2\sqrt{5}}{5}$.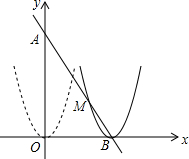 如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B.
如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B.