题目内容
13.对于函数y=x-1,下列结论不正确的是( )| A. | 图象经过点(-1,-2) | B. | 图象不经过第一象限 | ||
| C. | 图象与y轴交点坐标是(0,-1) | D. | y的值随x值的增大而增大 |
分析 根据一次函数图象上点的坐标特征对A、C进行判断;根据一次函数图象与系数的关系对B进行判断;根据一次函数的性质对D进行判断.
解答 解:A、当x=-1时,y=x-1=-1-1=-2,则图象经过点(-1,-2),所以A选项结论正确;
B、由于k>0,b<0,则图象经过第一、三、四象限,所以B选项结论错误;
C、当x=0时,y=-1,则图象与y轴交点交点坐标是(0,-1),所以C选项结论正确;
D、由于k=1>0,所以y的值随x值的增大而增大,所以D选项结论正确.
故选B.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.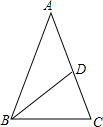 如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
 如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )| A. | 4 | B. | 4$\sqrt{5}$-4 | C. | -4$\sqrt{5}$+4 | D. | 4$\sqrt{5}$-4或-4$\sqrt{5}$+4 |
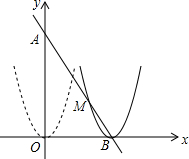 如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B.
如图,在平面直角坐标系中,点A(0,12),点B(6,0),抛物线y=x2沿O→B方向进行平移,平移后的抛物线顶点为B. 已知,如图,直线AB、CD相交于O,OE平分∠BOD且∠AOE=150°,∠AOC的度数为60°.
已知,如图,直线AB、CD相交于O,OE平分∠BOD且∠AOE=150°,∠AOC的度数为60°. 如图,已知直线a,b,c被直线d所截,若∠1=∠2,∠2+∠3=180°,求证:a∥c.
如图,已知直线a,b,c被直线d所截,若∠1=∠2,∠2+∠3=180°,求证:a∥c.