题目内容
11. 如图,已知直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则n的值是( )
如图,已知直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则n的值是( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 1.5 |
分析 先求出A、B两点的坐标,根据勾股定理得出AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5.再根据折叠的性质得出AB′=AB=5,B′C=BC=3-n.然后在直角△OB′C中,利用勾股定理列出方程(3-n)2=12+n2,解方程即可求出n的值.
解答 解:∵直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,
∴A(4,0),B(0,3),
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5.
∵把坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AB′=AB=5,B′C=BC=3-n.
在直角△OB′C中,∵∠B′OC=90°,OB′=5-4=1,OC=n,B′C=3-n,
∴(3-n)2=12+n2,
解得n=$\frac{4}{3}$.
故选C.
点评 本题考查了一次函数图象上点的坐标特征,折叠的性质,勾股定理,利用勾股定理列出方程(3-n)2=12+n2是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
1.y=-2(x+2)2-3的顶点坐标是( )
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
2.下列各数中,最小的数是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 0 | D. | $-\sqrt{2}$ |
19.调查某小区内30户居民月人均收入情况,制成如下频数分布直方图,且人均收入在1 200~1 240元的频数是( )


| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
3.在平面直角坐标系中,点A坐标为(4,5),点A向左平移5个单位长度到点A1,则点A1的坐标是( )
| A. | (-1,5) | B. | (0,5) | C. | (9,5) | D. | (-1,0) |
20.若2014$\sqrt{x+y-1}$+$\frac{1}{6}$(y+3)2=0,则x-y的值是( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
1.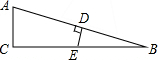 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )
 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
 如图,FB⊥AB,EC⊥AB,∠1=∠D=45°,则图中与∠CED相等的角共有4个.
如图,FB⊥AB,EC⊥AB,∠1=∠D=45°,则图中与∠CED相等的角共有4个.