题目内容
12．已知$\frac{A}{x+3}+\frac{B}{x-2}$计算结果是$\frac{3x+4}{（x+3）（x-2）}$，则常数A=1，B=2．分析 根据题目中的式子可以得到关于A和B的二元一次方程组，从而可以求得A、B的值．
解答 解：∵$\frac{A}{x+3}+\frac{B}{x-2}$计算结果是$\frac{3x+4}{（x+3）（x-2）}$，
∴$\frac{A}{x+3}+\frac{B}{x-2}=\frac{3x+4}{（x+3）（x-2）}$，
∴$\frac{A（x-2）+B（x+3）}{（x+3）（x-2）}=\frac{3x+4}{（x+3）（x-2）}$，
∴$\frac{（A+B）x+（-2A+3B）}{（x+3）（x-2）}=\frac{3x+4}{（x+3）（x-2）}$，
∴$\left\{\begin{array}{l}{A+B=3}\\{-2A+3B=4}\end{array}\right.$，
解得，$\left\{\begin{array}{l}{A=1}\\{B=2}\end{array}\right.$，
故答案为：1，2．
点评 本替考查分式的加减法、解二元一次方程组，解答本题的关键是明确它们各自的计算方法．
练习册系列答案
相关题目
2．下列各数中，最小的数是（ ）
| A． | -2 | B． | $\frac{1}{2}$ | C． | 0 | D． | $-\sqrt{2}$ |
3．在平面直角坐标系中，点A坐标为（4，5），点A向左平移5个单位长度到点A1，则点A1的坐标是（ ）
| A． | （-1，5） | B． | （0，5） | C． | （9，5） | D． | （-1，0） |
20．若2014$\sqrt{x+y-1}$+$\frac{1}{6}$（y+3）2=0，则x-y的值是（ ）
| A． | 1 | B． | -1 | C． | 7 | D． | -7 |
7．
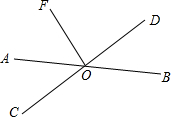如图，直线AB、CD相交于点O，OF⊥CO，∠AOF与∠BOD的度数之比为3：2，则∠AOC的度数是（ ）
如图，直线AB、CD相交于点O，OF⊥CO，∠AOF与∠BOD的度数之比为3：2，则∠AOC的度数是（ ）| A． | 18° | B． | 45° | C． | 36° | D． | 30° |
17．当$\frac{2a-5}{{\sqrt{a-3}}}$有意义时，a的取值范围是（ ）
| A． | a≥3 | B． | a＞3 | C． | a≠3 | D． | a≠-3 |
4．已知点A（-1，1）及点B（2，3），P是x轴上一动点，连接PA，PB，则PA+PB的最小值是（ ）
| A． | $\sqrt{13}$ | B． | 3$\sqrt{2}$ | C． | 5 | D． | 4 |
1．
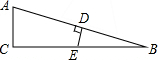如图，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交AB于D，交BC于E，若BE=8cm，则AC的长为（ ）
如图，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交AB于D，交BC于E，若BE=8cm，则AC的长为（ ）| A． | 4cm | B． | 5cm | C． | 6cm | D． | 8cm |
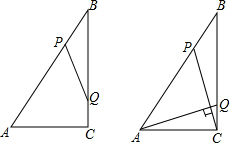如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．