题目内容
 如图,A、B两建筑物位于河的两岸,为了测量它们的距离,可以沿河岸作一条直线MN,且使MN⊥AB于点B,在BN上截取BC=CD,过点D作DE⊥MN,使点A、C、E在同一直线上,则DE的长就是A、B两建筑物之间的距离,请说明理由.
如图,A、B两建筑物位于河的两岸,为了测量它们的距离,可以沿河岸作一条直线MN,且使MN⊥AB于点B,在BN上截取BC=CD,过点D作DE⊥MN,使点A、C、E在同一直线上,则DE的长就是A、B两建筑物之间的距离,请说明理由.考点:全等三角形的应用
专题:
分析:可以沿河岸作射线BF,且使BF⊥AB,在BF上截取BC=CD,过D点作DE⊥BF,使E、C、A在一条直线上,证明出这两个三角形全等,从而可得到结论.
解答:解:∵AB⊥MN,
∴∠ABC=90°,
同理∠EDC=90°,
∴∠ABC=∠EDC,
在△ABC和△EDC中
∴△ACB≌△ECD(ASA),
∴AB=DE.
∴∠ABC=90°,
同理∠EDC=90°,
∴∠ABC=∠EDC,
在△ABC和△EDC中
|
∴△ACB≌△ECD(ASA),
∴AB=DE.
点评:本题考查全等三角形的应用,关键是证明三角形全等,从而得到线段相等,得到结论.

练习册系列答案
相关题目

 如图,点E是正方形内一点,△EDC是等边三角形
如图,点E是正方形内一点,△EDC是等边三角形 如图,在8×8的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
如图,在8×8的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
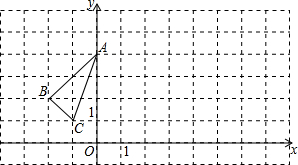 如图,已知在平面直角坐标系中,△ABC的位置如图.
如图,已知在平面直角坐标系中,△ABC的位置如图.