题目内容
16．
如图，在△ABC中，AC⊥BC，AD为∠BAC的平分线，DE⊥AB，AB=8cm，AC=3cm，求BE的长．
分析 先利用角平分线的定义得到DE=DC，再结合题中条件得出△ADE≌△ADC，从而可知AE=AC=6cm，所以求得BE=AB-AE=10-6=4cm．
解答 解：∵AD平分∠BAC，∠ACB=90°，DE⊥AB，
∴DE=DC．
在Rt△ADE与Rt△ADC中，$\left\{\begin{array}{l}{DE=CD}\\{AD=AD}\\{\;}\end{array}\right.$，
∴Rt△ADE≌Rt△ADC（HL），
∴AE=AC=3m，
∴BE=AB-AE=8-3=5cm．
点评 本题考查三角形全等的判定方法和全等三角形的性质及角平分线的性质，判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．证出DE=DC是证明三角形全等的前提．
练习册系列答案
单元期中期末卷系列答案
相关题目
如图所示，AB、CD是⊙O的直径，且AB⊥CD，E是OC的中点，过点E作FG∥AB交⊙O于F、G两点．求证：∠CBF=2∠ABF．
如图，在△ABC中．∠ABC=50°．∠ACB=60°．点E在BC的延长线上，∠ABC的平分线BD与∠ACE的平分线CD相交于点D．连接AD．则∠BAC=70°，∠BDC=35°，∠DAC=55°．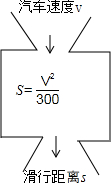
在平整的路面上．某型号汽车紧急刹车后仍将滑行S米，一般地有经验公式S=$\frac{{V}^{2}}{300}$，其中V表示刹车前汽车的速度（单位：千米/时）．