题目内容
4.已知△ABC是⊙O的内接三角形.(1)如图(1)若AC=2,∠ABC=30°,试求图中阴影部分的面积;
(2)如图(2),BD是⊙O的直径,AE⊥BC;
①求证:△AEC∽△BAD;
②若AB=$\sqrt{2}$,AD=2$\sqrt{2}$,∠ABC=45°,试求线段AC和BD的长.

分析 (1)根据等边三角形的判定得出△AOC是等边三角形,进而得出等边三角形的面积,再利用扇形AOC的面积公式,即可得出图中阴影部分的面积;
(2)根据BD是⊙O的直径,AE⊥BC,得到∠BAD=∠AEC=90°,由于∠D=∠C,根据相似三角形的判定即可得到结论;②根据等腰直角三角形的性质得到AE=BE=$\frac{\sqrt{2}}{2}$AB=1,根据勾股定理得到BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=$\sqrt{10}$,根据相似三角形的性质得到$\frac{AE}{AB}=\frac{AC}{BD}$,代入数据即可得到结论.
解答 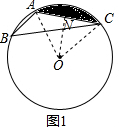 解:(1)如图1,连接AO,CO,过点O作ON⊥AC于点N,
解:(1)如图1,连接AO,CO,过点O作ON⊥AC于点N,
∵△ABC是⊙O的内接三角形,∠B=30°,
∴∠AOC=60°,
∵AO=CO,
∴△AOC是等边三角形,
∵AC=6,ON⊥AC,
∴AN=NC=1,
∴ON=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴△AOC的面积为:$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
扇形AOC的面积为:$\frac{60•π•{2}^{2}}{360}$=$\frac{2}{3}$π,
∴图中阴影部分的面积是:$\frac{2}{3}$π-$\sqrt{3}$;
(2)①∵BD是⊙O的直径,AE⊥BC,
∴∠BAD=∠AEC=90°,
∵∠D=∠C,
∴△AEC∽△BAD;
②∵∠ABC=45°,∠AEB=90°,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB=1,
∵∠BAD=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=$\sqrt{10}$,
∵△AEC∽△BAD,
∴$\frac{AE}{AB}=\frac{AC}{BD}$,
即$\frac{1}{\sqrt{2}}=\frac{AC}{\sqrt{10}}$,
∴AC=$\sqrt{5}$.
点评 此题主要考查了相似三角形的判定和性质,勾股定理,圆周角定理,等边三角形的判定,扇形面积求法,等边三角形面积求法,根据已知得出等边三角形的高是解决(1)题关键.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案 如图,一块直角三角板ABC,∠B=90°,AB=3,BC=4,截得两个正方形,DEFG、BDEF,设S1=DEFG的面积,S2=BDEF的面积,则S1、S2的大小关系是( )
如图,一块直角三角板ABC,∠B=90°,AB=3,BC=4,截得两个正方形,DEFG、BDEF,设S1=DEFG的面积,S2=BDEF的面积,则S1、S2的大小关系是( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 无法确定 |
 如图,已知平行四边形ABCD的对角线相交于点O,点E是边BC的中点,联结DE交AC于点G.设$\overrightarrow{AD}$=$\vec a$,$\overrightarrow{DC}$=$\vec b$,
如图,已知平行四边形ABCD的对角线相交于点O,点E是边BC的中点,联结DE交AC于点G.设$\overrightarrow{AD}$=$\vec a$,$\overrightarrow{DC}$=$\vec b$, 如图,点A、B、C在⊙O上,⊙O的半径为9,$\widehat{AB}$的长为2π,则∠ACB的大小是20°.
如图,点A、B、C在⊙O上,⊙O的半径为9,$\widehat{AB}$的长为2π,则∠ACB的大小是20°.