题目内容
16．已知△ABD≌△CDB，AD=BD，BE⊥AD于E，∠EBD=20°，则∠CDE的度数为125°或15°．分析 由直角三角形的性质求出∠BDA的度数，由等腰三角形的性质和三角形内角和定理求出∠A=∠ABD=55°，由全等三角形的性质得出∠CBD=∠BDA=70°，BC=BD，∠BDC=∠C=55°，分两种情况，即可得出结果．
解答 解：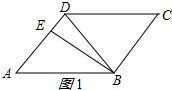
∵BE⊥AD于E，∠EBD=20°，
∴∠BDA=90°-20°=70°，
∵AD=BD，∴∠A=∠ABD=55°，
∵△ABD≌△CDB，
∴∠CBD=∠BDA=70°，BC=BD，∠BDC=∠C=55°，
分两种情况：
①如图1所示：∠CDE=70°+55°=125°；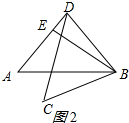
②如图2所示：∠CDE=70°-55°=15°；
综上所述：∠CDE的度数为125°或15°；
故答案为：125°或15°．
点评 本题考查了全等三角形的性质、直角三角形的性质、等腰三角形的性质、三角形内角和定理；根据题意画出图形，分两种情况讨论是解决问题的关键．
练习册系列答案
相关题目
16．已知a=5-2$\sqrt{6}$，则a2-10a+1的值是（ ）
| A． | -30$\sqrt{6}$ | B． | -18$\sqrt{6}$-2 | C． | 0 | D． | 10$\sqrt{6}$ |
如图，把含有30°角的三角板ABO置入平面直角坐标系中，A，B两点坐标分别为（3，0）和（0，3$\sqrt{3}$）．动点P从A点开始沿折线AO-OB-BA运动，点P在AO，OB，BA上运动，速度分别为1，$\sqrt{3}$，2（长度单位/秒）．一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$（长度单位/秒）的速度向上平行移动（即移动过程中保持l∥x轴），且分别与OB，AB交于E，F两点﹒设动点P与动直线l同时出发，运动时间为t秒，当点P沿折线AO-OB-BA运动一周时，直线l和动点P同时停止运动．
8．下列运算正确的是（ ）
| A． | 若x=y，则$\frac{x}{a}$=$\frac{y}{a}$ | B． | 若$\frac{x}{y}$（y≠0），则$\frac{xy}{{y}^{2}}$ | ||
| C． | 若$\frac{x}{y}$（y≠0），则$\frac{x+a}{y+a}$ | D． | 若x2=y2，则x=y |
如图，在△ABC中，∠C=90°，∠B=30°，AD是∠BAC的角平分线，DE⊥AB，垂足为E，DE=1，则BC=3．