题目内容
7. 如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'.若点B的对应点B'落在边CD上,则B'C的长为1.
如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'.若点B的对应点B'落在边CD上,则B'C的长为1.
分析 B′C=5-B′D.在直角△AB′D中,利用勾股定理求得B′D的长度即可.
解答  解:由旋转的性质得到AB=AB′=5,
解:由旋转的性质得到AB=AB′=5,
在直角△AB′D中,∠D=90°,AD=3,AB′=AB=5,
所以B′D=$\sqrt{AB{′}^{2}-A{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
所以B′C=5-B′D=1.
故答案是:1.
点评 本题考查了旋转的性质,矩形的性质.解题时,根据旋转的性质得到AB=AB′=5是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.一组数据5,7,8,10,12,12,44的众数是( )
| A. | 10 | B. | 12 | C. | 14 | D. | 44 |
15.如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
2.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | (a2)3=a6 | D. | (ab)2=ab2 |
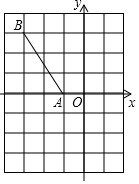 如图,线段AB的两个顶点都在方格纸的格点上,建立直角坐标系后点A的坐标是(-1,0),将线段AB绕点A顺时针旋转180°,则旋转后点B的对应点的坐标是(1,-3).
如图,线段AB的两个顶点都在方格纸的格点上,建立直角坐标系后点A的坐标是(-1,0),将线段AB绕点A顺时针旋转180°,则旋转后点B的对应点的坐标是(1,-3).