题目内容
13.计算(1)2$\sqrt{3}$-$\sqrt{8}$+$\frac{1}{2}$$\sqrt{12}$+$\frac{1}{5}$$\sqrt{50}$
(2)$\sqrt{15}$÷(-$\frac{1}{3}$$\sqrt{6}$)×$\frac{3}{5}$$\sqrt{20}$.
分析 (1)先把各个二次根式根据二次根式的性质化为最简二次根式,合并同类二次根式即可;
(2)根据二次根式的乘除运算法则计算即可.
解答 解:(1)原式=2$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{3}$+$\sqrt{2}$
=3$\sqrt{3}$-$\sqrt{2}$;
(2)原式=$\sqrt{15}$×(-$\frac{3}{\sqrt{6}}$)×$\frac{6\sqrt{5}}{5}$
=-$\frac{\sqrt{15}×18×\sqrt{5}}{5\sqrt{6}}$
=-$\frac{5\sqrt{3}×18×\sqrt{6}}{5\sqrt{6}×\sqrt{6}}$
=-9$\sqrt{2}$.
点评 本题考查的是二次根式的混合运算,掌握二次根式的性质、正确把各个二次根式化为最简二次根式是解题的关键.

练习册系列答案
相关题目
1. 已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )
 已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图所示,且其顶点的纵坐标为4,则关于x的方程|ax2+bx+c|=5的根的情况是( )| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 有四个实数根 |
5.已知点M(a,b)在第三象限,则点N(-b,a)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
 已知如图,D,E分别是△ABC的边AB,AC上的点,AD=3,AB=8,AE=4,AC=6.求证:△ADE∽△ACB.
已知如图,D,E分别是△ABC的边AB,AC上的点,AD=3,AB=8,AE=4,AC=6.求证:△ADE∽△ACB. 已知:如图,在?ABCD中,M、N是对角线BD上的两点,且BM=DN.
已知:如图,在?ABCD中,M、N是对角线BD上的两点,且BM=DN.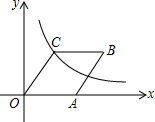 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).