已知二次函数y=ax2+bx+c的图象如图所示.且其顶点的纵坐标为4.则关于x的方程|ax2+bx+c|=5的根的情况是( )A．有两个相等的实数根B．有两个不相等的实数根C．没有实数根D．有四个实数根题目和参考答案——青夏教育精英家教网—

题目内容

1．

已知二次函数y=ax²+bx+c（a＜0）的图象如图所示，且其顶点的纵坐标为4，则关于x的方程|ax²+bx+c|=5的根的情况是（　　）

	A．	有两个相等的实数根		B．	有两个不相等的实数根
	C．	没有实数根		D．	有四个实数根

分析利用图象法：方程|ax²+bx+c|=5的根，可以看成直线y=5或直线y=-5与抛物线y=ax²+bx+c（a＜0）的图象的交点的横坐标，根据图象即可判断．

解答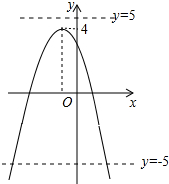解：如图所示，方程|ax²+bx+c|=5的根，可以看成直线y=5或直线y=-5与抛物线y=ax²+bx+c（a＜0）的图象的交点的横坐标，
由图象可知，有两个交点，
所以方程|ax²+bx+c|=5的根，有两个不相等的实数根．
故选B．

点评考查了抛物线与x轴的交点，解题的关键是利用图象法解决问题，体现了转化的思想，把求方程的根，转化为函数图象的交点问题，属于中考常考题型．

练习册系列答案

12．不等式-5x+12≥0的正整数解有（　　）

9．“鸟巢”的座席数是91000个，这个数用科学记数法表示为（　　）

16．

如图，己知抛物线y=$\frac{3}{8}$x²-$\frac{3}{4}$x-3与x轴交于A和B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．
（1）求出点A，B，D的坐标；
（2）如图，若线段OB在x轴上移动，且点O，B移动后的对应点为O′，B′，首尾顺次连接点O′、B′、D、C构成四边形O′B′DC，请求出四边形O′B′DC的周长最小值．

6．若x、y满足x²+y²=$\frac{5}{4}$，xy=-$\frac{1}{2}$，求下列各式的值．
（1）（x+y）²
（2）x⁴+y⁴．

13．计算
（1）2$\sqrt{3}$-$\sqrt{8}$+$\frac{1}{2}$$\sqrt{12}$+$\frac{1}{5}$$\sqrt{50}$
（2）$\sqrt{15}$÷（-$\frac{1}{3}$$\sqrt{6}$）×$\frac{3}{5}$$\sqrt{20}$．

10．

11．观察下列各式，并解答问题；
①$\frac{1}{2+\sqrt{2}}$=1-$\frac{\sqrt{2}}{2}$；②$\frac{1}{3\sqrt{2}+2\sqrt{3}}$=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{3}$；③$\frac{1}{4\sqrt{3}+3\sqrt{4}}$=$\frac{\sqrt{3}}{3}$-$\frac{\sqrt{4}}{4}$；④$\frac{1}{5\sqrt{4}+4\sqrt{5}}$=$\frac{\sqrt{4}}{4}$-$\frac{\sqrt{5}}{5}$
若n为正整数，用含n的等式来表示你探索的规律．

试题分类