Question

11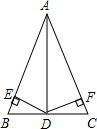．如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，BE=CF，由这些条件可以得出若干结论，请你写出其中三个正确的结论，并选其中一个结论证明（不要添加辅助线）．
（1）结论1∠B=∠C
结论2AB=AC
结论3AD⊥BC
（2）你选择证明的结论是：结论1
证明：
∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°，
在Rt△DEB和Rt△DFC中，
$\left\{\begin{array}{l}{BD=DC}\\{BE=CF}\end{array}\right.$，
∴Rt△DEB≌Rt△DFC，
∴∠B=∠C，．

Answer 1

分析 （1）结论是①∠B=∠C，②AB=AC，③AD⊥BC．
（2）根据HL证明△DEB≌△DFC即可解决问题．

解答 解：（1）结论是①∠B=∠C，②AB=AC，③AD⊥BC．
故答案为∠B=∠C，AB=AC，AD⊥BC．

（2）选择结论1证明：∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°，
在Rt△DEB和Rt△DFC中，
$\left\{\begin{array}{l}{BD=DC}\\{BE=CF}\end{array}\right.$，
∴Rt△DEB≌Rt△DFC，
∴∠B=∠C，
（其余结论，可以利用等腰三角形的性质进行证明）．
故答案为结论1．

点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是灵活运用全等三角形的判定和性质解决问题，属于基础题．