如图.在△ABC中.AB=AC.∠A=40°.BD是△ABC的角平分线.则∠ABD=35°．题目和参考答案——青夏教育精英家教网—

题目内容

1．

如图，在△ABC中，AB=AC，∠A=40°，BD是△ABC的角平分线，则∠ABD=35°．

分析由已知根据等腰三角形的性质易得两底角的度数，结合角平分线的性质和三角形内角和定理即可求解．

解答解：∵AB=AC，∠A=40°，
∴∠ABC=∠C=（180°-40°）÷2=70°，
又∵BD为∠ABC的平分线，
∴∠ABD=35°，
故答案为：35．

点评本题考查了三角形内角和定理及等腰三角形的性质、角平分线的性质；综合运用各种知识是解答本题的关键．

练习册系列答案

相关题目

11．

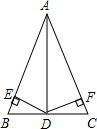如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，BE=CF，由这些条件可以得出若干结论，请你写出其中三个正确的结论，并选其中一个结论证明（不要添加辅助线）．
（1）结论1∠B=∠C
结论2AB=AC
结论3AD⊥BC
（2）你选择证明的结论是：结论1
证明：
∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°，
在Rt△DEB和Rt△DFC中，
$\left\{\begin{array}{l}{BD=DC}\\{BE=CF}\end{array}\right.$，
∴Rt△DEB≌Rt△DFC，
∴∠B=∠C，．

12．若分式$\frac{2y}{3x-3y}$中的x和y都扩大5倍，那么分式的值（　　）

9．

有理数a、b在数轴上的位置如图所示，则化简|a-b|-2|a+b|的绍果为a+3b．

16．A，B两地相距500千米，甲、乙两车分别从A，B两地同时出发，相向而行，已知甲的速度为110千米/时，乙车的速度为90千米/时，经过多少小时两车相距40千米？

6．

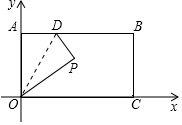如图，长方形OABC的边OC、OA分别在x轴、y轴上，点B的坐标为（$\sqrt{3}$，1）点D是AB边上一个动点（与点A不重合），沿OD将△OAD对折后，点A落到点P处，并满足△PCB是等腰三角形，则P点坐标为（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）或（$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）．

13．如果$\frac{a}{2}$=$\frac{b}{3}$（a≠0、b≠0），那么下列比例式变形错误的是（　　）

A．

$\frac{a}{b}=\frac{2}{3}$

B．

$\frac{b}{a}=\frac{3}{2}$

C．

$\frac{a}{b}=\frac{3}{2}$

D．

3a=2b

10．

如图，以等边△ABC的边BC为直径画半圆，分别交边AB、AC于点E，D，DF是半圆的切线，交AB于点F，若AF的长为1，则△FBC的面积为3$\sqrt{3}$．

11．下列比较大小的式子中，正确的是（　　）

试题分类