题目内容
4.已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )| A. | 等腰三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形 | D. | 等腰三角形或直角三角形 |
分析 等式两边乘以2,利用配方法得到(2a2-c2)2+(2b2-c2)2=0,根据非负数的性质得到2a2-c2=0,2b2-c2=0,则a=b,且a2+b2=c2.然后根据等腰三角形和直角三角形的判定方法进行判断.
解答 解:∵2a4+2b4+c4=2a2c2+2b2c2,
∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,
∴2a2-c2=0,2b2-c2=0,
∴c=$\sqrt{2}$a,c=$\sqrt{2}$b,
∴a=b,且a2+b2=c2.
∴△ABC为等腰直角三角形.
故选:B.
点评 本题考查了因式分解的应用,利用完全平方公式是解决问题的关键.

练习册系列答案
相关题目
19.-2015的绝对值是( )
| A. | -2015 | B. | 2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
9.一个正方形的面积是20,估计它的边长大小在( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
16. 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )
 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 三棱柱 | C. | 圆柱 | D. | 三棱锥 |
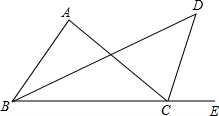 如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数.
如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数.