题目内容
3.△ABC中,AB=AC,BD为AC边上的中线,若BD等于△ABC的一边时,则tanC=$\frac{\sqrt{15}}{3}$或$\sqrt{7}$.分析 设AD=DC=x,则AB=AC=2x,设BC=4y.作AE⊥BC于E,DF⊥BC于F,根据等腰三角形三线合一的性质得出BE=EC=$\frac{1}{2}$BC=2y,由三角形中位线定理得出EF=FC=$\frac{1}{2}$EC=y.在直角△CDF与直角△BDF中,根据勾股定理求出DF2=CD2-FC2=x2-y2,BD2=DF2+BF2=x2-y2+(3y)2=x2+8y2.再分两种情况进行讨论:①如果BD等于腰长,根据BD=2x列出方程;②如果BD等于底边长,根据BD=4y列出方程.
解答 解:设AD=DC=x,则AB=AC=2x,设BC=4y.
作AE⊥BC于E,DF⊥BC于F,
∵AB=AC,
∴BE=EC=$\frac{1}{2}$BC=2y,
∵AD=DC,DF∥AE,
∴EF=FC=$\frac{1}{2}$EC=y.
在直角△CDF中,∵∠CFD=90°,
∴DF2=CD2-FC2=x2-y2,
在直角△BDF中,∵∠BFD=90°,
∴BD2=DF2+BF2=x2-y2+(3y)2=x2+8y2.
分两种情况: ①如果BD等于腰,即BD=2x,
①如果BD等于腰,即BD=2x,
则x2+8y2=4x2,
解得x2=$\frac{8}{3}$y2,
DF2=x2-y2=$\frac{5}{3}$y2,
在直角△CDF中,tanC=$\frac{DF}{FC}$=$\frac{\frac{\sqrt{15}}{3}y}{y}$=$\frac{\sqrt{15}}{3}$;
②BD等于底边,即BD=4y,
则x2+8y2=16y2,
解得x2=8y2,
DF2=x2-y2=7y2,
在直角△CDF中,tanC=$\frac{DF}{FC}$=$\frac{\sqrt{7}y}{y}$=$\sqrt{7}$.
故答案为$\frac{\sqrt{15}}{3}$或$\sqrt{7}$.
点评 本题考查了解直角三角形,等腰三角形的性质,勾股定理,锐角三角函数的定义,有一定难度.准确作出辅助线构造直角三角形,利用分类讨论、数形结合是解题的关键.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 如图,是我市几个旅游景点的大致位置示意图,如果用(-1,0)表示雨花塘的位置,用(1,5)表示杏花公园的位置,那么天鹅湖的位置可以表示为( )
如图,是我市几个旅游景点的大致位置示意图,如果用(-1,0)表示雨花塘的位置,用(1,5)表示杏花公园的位置,那么天鹅湖的位置可以表示为( )| A. | A(3,3) | B. | (-2,-3) | C. | (-3,-3) | D. | (-2,-2) |
| A. | 图形平移是由移动的方向和距离所决定的 | |
| B. | 图形旋转是由旋转中心和旋转角度所决定的 | |
| C. | 任意两点都成中心对称 | |
| D. | 任意两条相等的线段都成中心对称 |
 如图,反比例函数的图象经过点A(-2,5)和点B(-5,p),?ABCD的顶点C、D分别在y轴的负半轴、x轴的正半轴上,二次函数的图象经过点A、C、D.二次函数的解析式为y=x2-2x-3,若点E在对称轴右侧的二次函数图象上,且∠DCE>∠BDA,则点E的横坐标m的取值范围为1≤m<$\frac{9}{4}$或m>6.
如图,反比例函数的图象经过点A(-2,5)和点B(-5,p),?ABCD的顶点C、D分别在y轴的负半轴、x轴的正半轴上,二次函数的图象经过点A、C、D.二次函数的解析式为y=x2-2x-3,若点E在对称轴右侧的二次函数图象上,且∠DCE>∠BDA,则点E的横坐标m的取值范围为1≤m<$\frac{9}{4}$或m>6.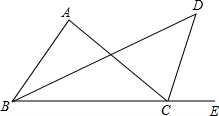 如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数.
如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数.