题目内容
20．计算（1）$\sqrt{81}$-$\root{3}{-125}$-$\sqrt{324}$
（2）（-2x2）2（$\frac{1}{2}$y）+3xy（1-$\frac{1}{3}$x3）-（3x3y）2÷x2y
（3）[（a-2b）2+（a-2b）（2b+a）-2a（2a-b）]÷2a．
分析 （1）先化简题目中的式子，然后根据有理数的加减法即可解答本题；
（2）根据积的乘方和同底数幂的乘法可以解答本题；
（3）根据完全平方公式和平方差公式、单项式乘多项式可以解答本题．
解答 解：（1）$\sqrt{81}$-$\root{3}{-125}$-$\sqrt{324}$
=9-（-5）-18
=9+5-18
=-4；
（2）（-2x2）2（$\frac{1}{2}$y）+3xy（1-$\frac{1}{3}$x3）-（3x3y）2÷x2y
=$（4{x}^{4}）•（\frac{1}{2}y）+3xy-{x}^{4}y-（9{x}^{6}{y}^{2}）÷{x}^{2}y$
=2x4y+3xy-x4y-9x4y
=-8x4y+3xy；
（3）[（a-2b）2+（a-2b）（2b+a）-2a（2a-b）]÷2a
=[a2-4ab+4b2+a2-4b2-4a2+2ab]÷2a
=（-2a2-2ab）÷2a
=-a-b．
点评 本题考查整式的混合运算、实数的运算，解答本题的关键是明确它们各自的计算方法．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
11．方程2x2+1=3x的两个根为（ ）
| A． | x1=2，x2=1 | B． | x1=$\frac{1}{2}$，x2=1 | C． | x1=-2，x2=1 | D． | x1=-$\frac{1}{2}$，x2=1 |
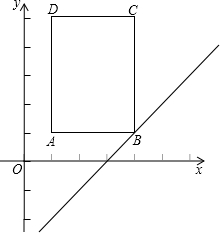如图，矩形ABCD在平面直角坐标系中，点A（1，1），B（4，1），C（4，5），D（1，5），将一次函数y=x-3的图象L沿y轴以每秒1个单位的速度向上运动，设运动的时间为t秒，L扫过矩形的面积为S．
5．
如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是x=1，下列结论：①b2＞4ac；②ac＞0； ③a-b+c＞0； ④不等式ax2+bx+c＞0的解集是-1＜x＜3；⑤当x＞1时，y随x的增大而减小，其中结论正确的序号是（ ）
如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是x=1，下列结论：①b2＞4ac；②ac＞0； ③a-b+c＞0； ④不等式ax2+bx+c＞0的解集是-1＜x＜3；⑤当x＞1时，y随x的增大而减小，其中结论正确的序号是（ ）| A． | ①②③ | B． | ①④⑤ | C． | ③④⑤ | D． | ①③⑤ |
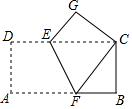如图，已知矩形ABCD，将纸片折叠，使顶点A与C重合，折痕EF分别于DC，AB交于E，F．