题目内容
 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是中线,CF是∠ACB的平分线,图中相等的锐角为一组,则共有
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是中线,CF是∠ACB的平分线,图中相等的锐角为一组,则共有考点:三角形内角和定理
专题:
分析:根据三角形内角和定理求出∠B=∠ACD,∠A=∠BCD,根据直角三角形的性质求出AE=CE=BE,求出∠A=∠ACE,∠B=∠BCE,根据角平分线定义求出∠ACF=∠BCF,即可得出答案.
解答:解:∵CD是AB边上的高,
∴∠ADC=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,∠A+∠ACD=90°,
∴∠B=∠ACD,
同理∠A=∠BCD,
∵∠ACB=90°,CE是中线,
∴AE=CE,CE=BE,
∴∠A=∠ACE,∠B=∠BCE,
∵CF是∠ACB的平分线,
∴∠ACF=∠BCF,
∵∠ACE=∠A=∠BCD,
∴∠2=∠1,
即∠DCB=∠A,∠A=∠ACE,∠DCB=∠ACE,∠B=∠ACD,∠ACF=∠BCF,∠1=∠2,∠B=∠BCE,∠BCE=∠ACD,共8组,
故答案为:8.
∴∠ADC=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,∠A+∠ACD=90°,
∴∠B=∠ACD,
同理∠A=∠BCD,
∵∠ACB=90°,CE是中线,
∴AE=CE,CE=BE,
∴∠A=∠ACE,∠B=∠BCE,
∵CF是∠ACB的平分线,
∴∠ACF=∠BCF,
∵∠ACE=∠A=∠BCD,
∴∠2=∠1,
即∠DCB=∠A,∠A=∠ACE,∠DCB=∠ACE,∠B=∠ACD,∠ACF=∠BCF,∠1=∠2,∠B=∠BCE,∠BCE=∠ACD,共8组,
故答案为:8.
点评:本题考查了垂直定义,角平分线定义,三角形的内角和定理,直角三角形斜边上中线的性质,等腰三角形的性质的应用,能综合运用性质进行推理是解此题的关键,有一定的难度.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、数轴上距离原点2个单位长度的点表示的数是2 |
| B、-1是最大的负整数 |
| C、任何有理数的绝对值都大于0 |
| D、0是最小的有理数 |
如图,三视图描述的实物形状是( )


| A、棱柱 | B、棱锥 | C、圆柱 | D、圆锥 |
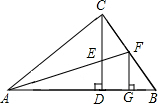 如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、BC于点E、F.且FG⊥AB,垂足为G,
如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、BC于点E、F.且FG⊥AB,垂足为G,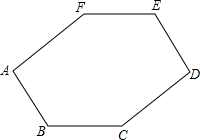 如图,在六边形ABCDEF中,∠C=∠F,∠A=∠D,BC∥EF.
如图,在六边形ABCDEF中,∠C=∠F,∠A=∠D,BC∥EF.