题目内容
19.已知∠α和∠β以及线段a,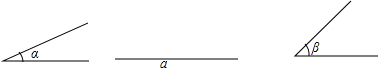
(1)用直尺和圆规求作△ABC,要求∠A=∠α,∠B=∠β,AC=a;
(2)用直尺和圆规作AB边的高CD;
(3)若a=10,sinα=$\frac{3}{5}$,tanβ=$\frac{3}{2}$,求出你所作的△ABC的面积的大小.
分析 (1)首先得出∠ACB=180°-α-β,进而作出∠A=α,AC=a,进而求出即可;
(2)过点C作CD⊥AB于点D,即可得出答案;
(3)利用锐角三角函数关系得出DC,AB的长进而得出答案.
解答  解:(1)如图所示:△ABC即为所求;
解:(1)如图所示:△ABC即为所求;
(2)如图所示:CD即为所求;
(3)∵CD⊥AB,a=10,sinα=$\frac{3}{5}$,
∴CD=6,
∴AD=8,
∵tanβ=$\frac{3}{2}$,
∴BD=4,
∴AB=12,
∴S△ABC=$\frac{1}{2}$×12×6=36.
点评 此题主要考查了复杂作图以及锐角三角函数关系,作出∠ACB=180°-α-β是解题关键.

练习册系列答案
相关题目
11.下列各等式正确的是( )
| A. | a3•a2=a6 | B. | (x3)2=x6 | C. | (mn)3=mn3 | D. | b8÷b4=b2 |
 如图,已知∠1=70°,如果CD∥BE,那么∠B=110°.
如图,已知∠1=70°,如果CD∥BE,那么∠B=110°.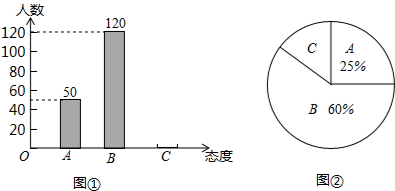

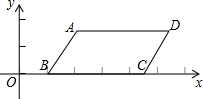 如图,在平行四边形ABCD中,已知A、B、C三点坐标分别为A(1+$\sqrt{3}$,$\sqrt{3}$),B(1,0),C(1+2$\sqrt{3}$,0)
如图,在平行四边形ABCD中,已知A、B、C三点坐标分别为A(1+$\sqrt{3}$,$\sqrt{3}$),B(1,0),C(1+2$\sqrt{3}$,0)