题目内容
7.先化简,再求值:$(\frac{3x}{x-1}-\frac{x}{x+1})÷\frac{{{x^4}-4{x^2}}}{{{x^3}-x}}$,其中$x=\sqrt{2}+2$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{3x(x+1)-x(x-1)}{(x-1)(x+1)}$•$\frac{x(x+1)(x-1)}{{x}^{2}(x+2)(x-2)}$
=$\frac{2x(x+2)}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x(x+2)(x-2)}$
=$\frac{x}{x-2}$,
当x=$\sqrt{2}$+2时,原式=$\frac{\sqrt{2}+2}{\sqrt{2}+2-2}$=1+$\sqrt{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
18.关于正比例函数y=-3x,下列结论中不正确的是( )
| A. | 不论x为何值,总有y<0 | B. | y随x的增大而减小 | ||
| C. | 图象经过点(1,-3) | D. | 图象经过第二、四象限 |
2.观察表格,由表格可得a=1,b=-2,c=3.
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | 3 | 3 |
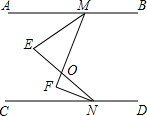 如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于O点
如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于O点