题目内容
14.若a、b、c是△ABC的三边,且a=6,b=8,c=10,则△ABC最长边上的高等于4.8.分析 先根据勾股定理的逆定理判断出△ABC为直角三角形,且最长边为c=10,再通过三角形的面积公式列出方程,化简计算即可得出答案.
解答 解:∵a、b、c是△ABC的三边,且a=6,b=8,c=10,
又62+82=102,
∴△ABC是直角三角形,且6,8是两条直角边的长,10为斜边的长,
设斜边上的高为h,则S△=$\frac{1}{2}$×6×8=$\frac{1}{2}$×10h,
解得h=4.8.
故答案为4.8.
点评 本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了直角三角形的面积.判断出△ABC为直角三角形是解题的关键.

练习册系列答案
相关题目
4.-9的绝对值等于( )
| A. | -9 | B. | 9 | C. | -$\frac{1}{9}$ | D. | $\frac{1}{9}$ |
2.观察表格,由表格可得a=1,b=-2,c=3.
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | 3 | 3 |
9.已知$m=\sqrt{2}+1$,$n=\sqrt{2}-1$,则$\sqrt{{m^2}+{n^2}-3mn}$=( )
| A. | 9 | B. | $\sqrt{3}$ | C. | 3 | D. | 5 |
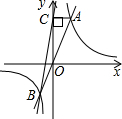 如图,直线y=kx与双曲线y=$\frac{m}{x}$相交于A,B两点,点A在第一象限,过点A作AC⊥y轴,垂足为点C,若AC=1,△BOC的面积是1,解答下列问题:
如图,直线y=kx与双曲线y=$\frac{m}{x}$相交于A,B两点,点A在第一象限,过点A作AC⊥y轴,垂足为点C,若AC=1,△BOC的面积是1,解答下列问题: