题目内容
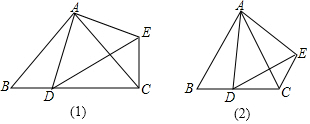
8.(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
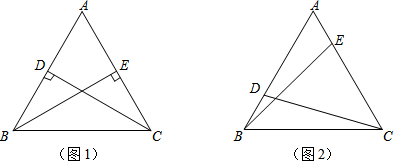
分析 (1)只要用全等判定“AAS”证明△ABE≌△ACD,则CD=BE易求;
(2)作CF⊥AB,BG⊥AC,根据全等三角形的性质得到CF=BG,推出△CFD≌△BGE,于是得到结论.
解答 (1)证明:∵CD⊥AB于点D,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE与△ACD中,$\left\{\begin{array}{l}{∠A=∠A}\\{∠ADC=∠AEB}\\{AB=AC}\end{array}\right.$,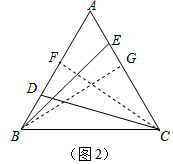
∴△ABE≌△ACD(AAS).
∴CD=BE;
(2)CD=BE,
证明如下:分别作CF⊥AB,BG⊥AC,
∴∠CBF=90°,∠BGC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中,$\left\{\begin{array}{l}{∠CBF=∠BGC}\\{∠ABC=∠ACB}\\{BC=BC}\end{array}\right.$,
∴△FBC≌△GCB.
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中,$\left\{\begin{array}{l}{∠FDC=∠BEG}\\{∠CBF=∠BGE}\\{CF=BG}\end{array}\right.$,
∴△CFD≌△BGE,
∴CD=BE.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列命题中,是真命题的是( )
| A. | 两个锐角的和是锐角 | |
| B. | 邻补角是互补的角 | |
| C. | 同旁内角互补 | |
| D. | 两条直线被第三条直线所截,内错角相等 |
3.已知青椒每斤3元,西红柿每斤2元,小张妈妈以每斤2.5元混合买了a斤青椒和b斤西红柿,结果小张发现妈妈亏钱了,原因是( )
| A. | a<b | B. | a>b | C. | a=b | D. | 与a,b大小无关 |
17.对于任意的实数x,代数式x2-5x+10的值是一个( )
| A. | 正数 | B. | 负数 | C. | 非负数 | D. | 不能确定 |
18.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 正五角星 | D. | 正六边形 |
 如图,B、F、C、E在一条直线上,AB=DE,BF=CE,AC=DF.
如图,B、F、C、E在一条直线上,AB=DE,BF=CE,AC=DF.