题目内容
9．
有一个数值转换器，程序如图，当输入的x为25时，输出的y是（ ）| A． | 5 | B． | -5 | C． | $\sqrt{5}$ | D． | -$\sqrt{5}$ |
分析 令x=25，然后根据程序图判断是有理数还是无理数，若无理数即可输出y
解答 解：x=25时，其算术平方根为5，为有理数，
x=5时，其算术平方根为$\sqrt{5}$，为无理数，
输出y=$\sqrt{5}$
故选（C）
点评 本题考查算术平方根，解题的关键是正确理解程序图的意义，本题属于基础题型．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
11．下列运算，正确的是（ ）
| A． | $\sqrt{20}$=2$\sqrt{10}$ | B． | $\sqrt{4}$-$\sqrt{2}$=$\sqrt{2}$ | C． | $\sqrt{（-3）^{2}}$=-3 | D． | $\sqrt{3}$•$\sqrt{2}$=$\sqrt{6}$ |
12．下面各种说法中正确的是（ ）
| A． | 两数的差一定小于被减数 | |
| B． | 两数的和一定大于每一个加数 | |
| C． | 两数的绝对值相等，这两个数也一定相等 | |
| D． | 两数的积不一定比每一个因数大 |
9．下列说法中正确的是（ ）
| A． | 近似数11.30是精确到个位的数 | |
| B． | 近似数41.3是精确到十分位的数 | |
| C． | 近似数五百和近似数500的精确度是相同的 | |
| D． | 近似数1.7和1.70是一样的 |
4．
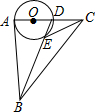如图，△ABC中，∠BAC=90°，AB=AC=2，D为AC上一动点，以AD为直径的⊙O交BD于E，则线段CE的最小值为（ ）
如图，△ABC中，∠BAC=90°，AB=AC=2，D为AC上一动点，以AD为直径的⊙O交BD于E，则线段CE的最小值为（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{5}$+1 | C． | 2$\sqrt{5}$ | D． | $\sqrt{5}$-1 |
14．
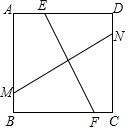如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、C D、A D、BC上．小明认为：若MN=EF，则MN⊥EF；小亮认为：若MN丄EF，则MN=EF，你认为（ ）
如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、C D、A D、BC上．小明认为：若MN=EF，则MN⊥EF；小亮认为：若MN丄EF，则MN=EF，你认为（ ）| A． | 两人都对 | B． | 仅小亮对 | C． | 仅小明对 | D． | 两人都不对 |
1．下列条件中，不能判断两个三角形全等的方法有（ ）
| A． | 两边和一个角分别相等的两个三角形 | |
| B． | 两个角及其夹边分别相等的两个三角形 | |
| C． | 三边分别相等的两个三角形 | |
| D． | 斜边和一条直角边分别相等的两个直角三角形 |
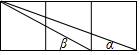如图，在边长为1的正方形网格内连结不同的对角线得到∠α和∠β，则∠α+∠β=45度．
如图，∵∠1=∠2，∴AB∥DE（同位角相等，两直线平行）