题目内容
20.任画一个直角三角形,分别以它的三条边为边向外作等边三角形,要求:(1)画出图形;
(2)探究这三个等边三角形面积之间的关系,并说明理由.
分析 (1)根据题意画出图形即可;
(2)利用直角△ABC的边长就可以表示出等边三角形S1、S2、S3的大小,由勾股定理,即可得出结果.
解答 解:(1)如图1所示;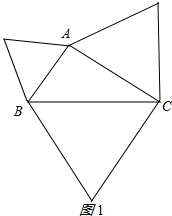
(2)如图2所示:
斜边所在等边三角形的面积是另外两个等边三角形面积之和,
即S1+S2=S3,
理由如下:
∵△ABC是直角三角形,
∴AB2+AC2=BC2,
∵S3=$\frac{\sqrt{3}}{4}$BC2,S1=$\frac{\sqrt{3}}{4}$AB2,
S2=$\frac{\sqrt{3}}{4}$AC2,
∴S1+S2=$\frac{\sqrt{3}}{4}$(AB2+AC2)=$\frac{\sqrt{3}}{4}$AB2=S3.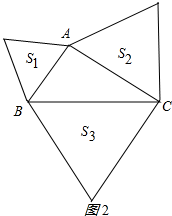
点评 本题考查了勾股定理、等边三角形的性质;熟练掌握等边三角形面积的计算公式,运用勾股定理得出面积关系是解决问题的关键.,

练习册系列答案
相关题目