题目内容
12.在半径为25cm的⊙O中,弦AB=40cm,则此弦和弦所对的弧的中点的距离是10cm和40cm.分析 点C和D为弦AB所对弧的中点,连结CD交AB于E,连结OA,如图,根据垂径定理的推论得到CD为直径,CD⊥AB,则AE=BE=$\frac{1}{2}$AB=20,再利用勾股定理计算出OE=15,然后分别计算出DE和CE即可.
解答 解: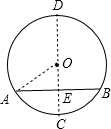 点C和D为弦AB所对弧的中点,连结CD交AB于E,连结OA,如图,
点C和D为弦AB所对弧的中点,连结CD交AB于E,连结OA,如图,
∵点C和D为弦AB所对弧的中点,
∴CD为直径,CD⊥AB,
∴AE=BE=$\frac{1}{2}$AB=20,
在Rt△OAE中,∵OA=25,AE=20,
∴OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=15,
∴DE=OD+OE=40,CE=OC-OE=10,
即弦AB和弦AB所对的劣弧的中点的距离为10cm,弦AB和弦AB所对的优弧的中点的距离为40cm.
故答案为10cm和40cm.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
7.已知-2<m<3,化简$\sqrt{(m-3)^{2}}$+|m+2|的结果是( )
| A. | 5 | B. | 1 | C. | 2m-1 | D. | 2m-5 |
 将已知线段AB分成1:2:3三部分(写出作法).
将已知线段AB分成1:2:3三部分(写出作法).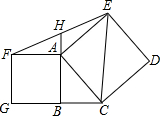 已知:如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向△ABC外作正方形ACDE和正方形ABGF,连接EF、EC,延长BA交EF于H.
已知:如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向△ABC外作正方形ACDE和正方形ABGF,连接EF、EC,延长BA交EF于H.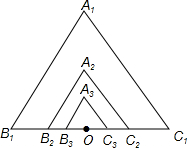 如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.
如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.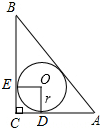 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=1.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=1.