题目内容
2.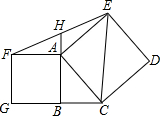 已知:如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向△ABC外作正方形ACDE和正方形ABGF,连接EF、EC,延长BA交EF于H.
已知:如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向△ABC外作正方形ACDE和正方形ABGF,连接EF、EC,延长BA交EF于H.(1)若tan∠ACB=$\frac{2}{3}$,S△ABC=12,求EC的长;
(2)求证:BC=2AH.
分析 (1)由tan∠ACB=$\frac{AB}{BC}$=$\frac{2}{3}$,设AB=2x,BC=3x,根据S△ABC=$\frac{1}{2}$AB•BC,得出x=2,AB=4,BC=6,由勾股定理求出AC,再根据正方形的性质得出EC=$\sqrt{2}$AC,即可得出结果;
(2)过E作EM∥AF,交AH的延长线于M,连接FM,先证明△ABC≌△AEM,得出AB=EM,MA=BC,再证出FA=EM,得出四边形AEMF是平行四边形,得出MH=AH=$\frac{1}{2}$MA,即可得出结论.
解答 解:(1)∵tan∠ACB=$\frac{AB}{BC}$=$\frac{2}{3}$,
∴设AB=2x,BC=3x,
∴S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×2x•3x=12,
解得:x=$\sqrt{4}$=2,
∴AB=4,BC=6,
∴AC=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∵四边形ACDE是正方形,
∴∠CAE=90°,AE=AC=2$\sqrt{13}$,
∴EC=$\sqrt{2}$AC=2$\sqrt{26}$;
(2)过E作EM∥AF,交AH的延长线于M,连接FM,如图所示: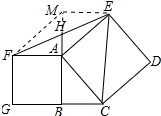 则∠AME=∠FAM,
则∠AME=∠FAM,
∵四边形ABGF是正方形,
∴∠BAF=90°,AB=AF,
∴∠FAM=∠AME=90°,
∵∠MAE+∠EAC+∠CAB=180°,∠EAC=90°,
∴∠MAE+∠CAB=90°,
在△ABC中,∠BCA+∠CAB=90°,
∴∠MAE=∠BCA,
在△ABC和△AEM中,
$\left\{\begin{array}{l}{∠ABC=∠AME}&{\;}\\{∠MAE=∠BCA}&{\;}\\{AC=AE}&{\;}\end{array}\right.$,
∴△ABC≌△AEM(AAS),
∴AB=EM,MA=BC,
∵AB=AF,
∴FA=EM,
∵EM∥AF,
∴四边形AEMF是平行四边形,
∴MH=AH=$\frac{1}{2}$MA,
∴BC=2AH.
点评 本题考查了正方形的性质、全等三角形的判定与性质、平行四边形的判定与性质以及勾股定理;本题有一定难度,特别是(2)中,需要通过作辅助线证明三角形全等和平行四边形才能得出结论.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.
如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.
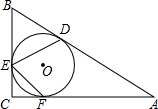 如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°.
如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°.