题目内容
13．
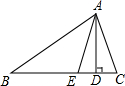如图，在△ABC中，AD⊥BC于D，AE为∠BAC的平分线，且∠DAE=15°，∠B=35°，则∠C=65°．
分析 利用三角形内角和定理求得∠AED=75°；然后根据已知条件和三角形外角定理可以求得∠BAE的度数；最后结合三角形角平分线的定义和三角形内角和定理进行解答．
解答 解：如图，∵AD⊥BC，
∴∠ADE=90°．
又∵∠DAE=15°，
∴∠AED=75°．
∵∠B=35°，
∴∠BAE=∠AED-∠B=40°．
又∵AE为∠BAC的平分线，
∴∠BAC=2∠BAE=80°，
∴∠C=180°-∠B-∠BAC=65°．
故答案是：65．
点评 本题主要考查三角形内角和定理，垂直的性质，角平分线的性质，关键在于熟练运用个性质定理推出相关角之间的关系．
练习册系列答案
相关题目
如图所示，在△ABC中，AB=AC，在AB上取一点E，在AC延长线上取一点F，使BE=CF，EF交BC于G．求证：EG=FG．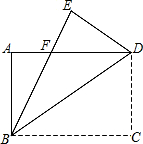
如图，有一个直角三角形纸片，两直角边AB=6cm，BC=8cm，现将直角边BC沿直线BD折叠，使点C落在点E处，求三角形BDF的面积是多少？
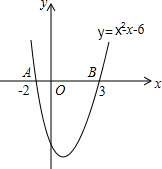观察二次函数y=x2-x-6的图象，回答问题：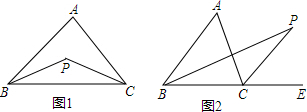
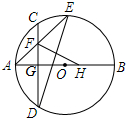如图，AB是⊙O的直径，点A为$\widehat{CD}$的中点，点F是CG的中点，AF的延长线交⊙O于点E，点H是BG的中点，tanE=$\frac{1}{2}$．