题目内容

13．在△ABC中，∠A、∠B、∠C 所对的边分别是a、b、c，且a2=b2-c2，那么（　　）
A．∠A是直角B．∠B是直角C．∠C是直角D．以上都不对

分析 根据a2=b2-c2，得出b2=a2+c2，再根据勾股定理的逆定理得出∠B=90°．

解答 解：∵a2=b2-c2，
∴b2=a2+c2，
∴△ABC是直角三角形，且∠B=90°，
∴∠B是直角．
故选：B．

点评 此题考查了勾股定理的逆定理，如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形，且最长边所对的角是直角．

练习册系列答案
相关题目
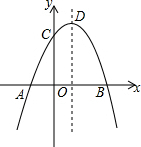3．如图，抛物线y=-x2+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D．下列四个命题：①当x＞0时，y＞0； ②若a=-1，则b=3；③抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2；④点C关于抛物线对称轴 的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为6$\sqrt{2}$．其中正确的命题有（　　）个．
A．1B．2C．3D．4
4．下列语句叙述正确的个数是（　　）
①横坐标与纵坐标互为相反数的点在直线y=-x上；   
②点P（2，0）在y轴上；
③若点P的坐标为（a，b），且ab=0，则P点是坐标原点；
④函数y=1-x中y随x的增大而增大．
A．1个B．2个C．3个D．4个
1．若|a|=2，b=3，且ab＜0，求a-b的值？
8．（1）-12-（-10）÷$\frac{1}{2}×2+{（{-4}）^2}$
（2）（2$\frac{1}{3}-3\frac{1}{2}+1\frac{4}{45}$）÷（-1$\frac{1}{6}$）
18．已知a+$\frac{1}{a}$=$\sqrt{5}$，则a-$\frac{1}{a}$=（　　）
A．1B．-1C．±1D．-$\sqrt{5}$
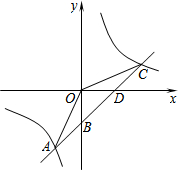5．如图，一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2，-5﹚，C﹙5，n﹚，交y轴于点B，交x轴于点D．
（1）求反比例函数$y=\frac{m}{x}$和一次函数y=kx+b的表达式；
（2）连接OA，OC，求△AOC的面积；
（3）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．
2．先化简，再求值：$\frac{1}{2}$x-[-2（x-$\frac{2}{3}$y2）-（-$\frac{5}{2}$x+$\frac{1}{3}$y2）-x]-y2，其中$x=-\frac{1}{2}$，$y=-\frac{1}{2}$．
3．△ABC中，BC=AC，D是AB上一点，连结CD，且AD=BD=CD，则∠A的度数为（　　）
A．45°B．36°C．90°D．135°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网